某地区的一种特色水果上市时间仅能持续5个月,预测上市初期和后期会因供不应求使价格呈连续上涨态势,而中期又将出现供大于求使价格下跌.现有三种价格模拟函数:①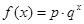 ;②
;②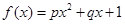 ;③
;③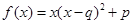 .(以上三式中
.(以上三式中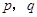 均为常数,且
均为常数,且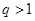 )
)
(1)为准确研究其价格走势,应选哪种价格模拟函数,为什么?
(2)若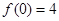 ,
,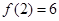 ,求出所选函数
,求出所选函数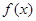 的解析式(注:函数的定义域是
的解析式(注:函数的定义域是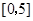 ).其中
).其中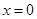 表示4月1日,
表示4月1日,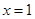 表示5月1日,…,依此类推;
表示5月1日,…,依此类推;
(3)为保护果农的收益,打算在价格下跌期间积极拓宽外销,请你预测该果品在哪几个月内价格下跌.
已知数列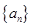 的前
的前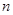 项和
项和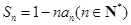 .
.
(1)计算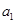 ,
,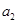 ,
,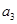 ,
,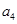 ;
;
(2)猜想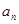 的表达式,并用数学归纳法证明你的结论
的表达式,并用数学归纳法证明你的结论
已知抛物线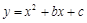 在点
在点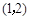 处的切线与直线
处的切线与直线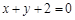 垂直,求函数
垂直,求函数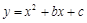 的最值.
的最值.
已知复数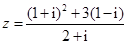 ,若
,若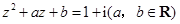 ,求
,求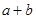 的值.
的值.
已知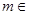 R,函数
R,函数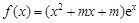 .
.
⑴若函数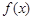 没有零点,求实数
没有零点,求实数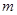 的取值范围;
的取值范围;
⑵若函数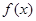 存在极大值,并记为
存在极大值,并记为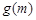 ,求
,求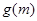 的表达式;
的表达式;
⑶当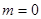 时,求证:
时,求证: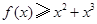 .
.