如图(甲),MN、PQ两条平行的光滑金属轨道与水平面成θ = 30°角固定,M、P之间接电阻箱R,电阻箱的阻值范围为0~4Ω,导轨所在空间存在匀强磁场,磁场方向垂直于轨道平面向上,磁感应强度为B = 0.5T。质量为m的金属杆a b水平放置在轨道上,其接入电路的电阻值为r。现从静止释放杆a b,测得最大速度为vm。改变电阻箱的阻值R,得到vm与R的关系如图(乙)所示。已知轨距为L = 2m,重力加速度g=l0m/s2,轨道足够长且电阻不计。
(1)当R =0时,求杆a b匀速下滑过程中产生感生电动势E的大小及杆中的电流方向;
(2)求金属杆的质量m和阻值r;
(3)求金属杆匀速下滑时电阻箱消耗电功率的最大值Pm。
在空中O点,每隔0.1s从静止释放一相同小球,小球的体积极小,可视为质点.在连续释放几个小球后,某一瞬间拍摄在空中运动的几个小球的照片是按1:40比例拍摄的,现用刻度尺去测量照片上小球A、B、C、D之间的距离,如图,试求:
(1)小球下落的加速度多大?
(2)从照片推测,在A球上面,正在空中下落的小球有几个?
一个物体从45m高的地方静止释放,做自由落体运动,(g取10m/s2)求:
(1)到达地面时的速度
(2)下落第1秒和最后1s内的位移.
一质点从静止开始以1m/s2的加速度匀加速直线运动,运动5s后做匀速直线运动,最后2s的时间内质点做匀减速直线运动直至静止,运动的总时间是12s.求:
(1)质点做匀速直线运动时的速度是多大?
(2)匀减速直线运动的加速度?
(3)质点运动的总位移多大?
滑板车运动,是青年学生喜爱的一项体育运动.某次比赛过程中,某同学乘滑板车比赛的过程简化如下:在平直的赛道上,自O点由静止开始做匀加速直线运动,途中6s时间内依次经过P、Q两根标志杆,已知P、Q相距60m,滑板车经过Q时的速率为15m/s,求:
(1)滑板车经过P时的速率vp?
(2)滑板车的加速度为多少?
(3)O、P间的距离为多少?(将滑板车和同学视为质点)
刹车距离(即图中“减速过程”所经过的位移),是评价汽车安全性能的一个重要指标.某型号骑车在一段马路上的测试结果是:当骑车以15m/s速度匀速行驶时,从开始到汽车停下的距离是10米.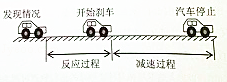
(1)求测试骑车减速时的加速度为多大?
(2)假设一般人的刹车反应时间(即图中“反应过程”所用时间t0=0.5s.若在测试车前方摆放一固定障碍物,那么测试司机至少应在多远处发现目标才不至于出现安全事故.