(19分)如图所示，带正电的绝缘小滑块A，被长R=0.4m的绝缘细绳竖直悬挂，悬点O距水平地面的高度为3R；小滑块B不带电．位于O点正下方的地面上。长L=2R的绝缘水平传送带上表面距地面的高度h=2R，其左端与O点在同一竖直线上，右端的右侧空间有方向竖直向下的匀强电场。在O点与传送带之间有位置可调的固定钉子(图中未画出)，当把A拉到水平位置由静止释放后，因钉子阻挡，细绳总会断裂，使得A能滑上传送带继续运动，若传送带逆时针匀速转动，A刚好能运动到传送带的右端。已知绝缘细绳能承受的最大拉力是A重力的5倍，A所受电场力大小与重力相等，重力加速度g=10m／s2，A.B均可视为质点，皮带传动轮半径很小，A不会因绳断裂而损失能量、也不会因摩擦而损失电荷量。试求：
(1)钉子距O点的距离的范围。
(2)若传送带以速度v0=5m／s顺时针匀速转动，在A刚滑到传送带上时，B从静止开始向右做匀加速直线运动，当A刚落地时，B恰与A相碰。试求B做匀加速运动的加速度大小(结果可用根式表示)
质量为M=2.5kg的一只长方体形状的铁箱在水平拉力F作用下沿水平面向右匀加速运动，铁箱与水平面间的动摩擦因数为μ1=0.50。这时铁箱内一个质量为m=0.5kg的木块恰好能静止在后壁上(如图所示)，木块与铁箱内壁间的动摩擦因数为μ2=0.25。设最大静摩擦力等于滑动摩擦力，g取10m/s2。
求：(1)木块对铁箱的压力；
(2)水平拉力F的大小；
(3)使拉力F减小到120N，经过一段时间，木块落至箱底后且不反弹，某时刻当箱的速度为v=6m/s时撤去拉力，经1s时间木块从左侧到达右侧，则铁箱长度是多少？
如图所示，在高出水平地面
的光滑平台上放置一质量
、由两种不同材料连接成一体的薄板A，其右段长度
且表面光滑，左段表面粗糙。在A最右端放有可视为质点的物块B，其质量
。B与A左段间动摩擦因数
。开始时二者均静止，现对A施加
水平向右的恒力，待B脱离A（A尚未露出平台）后，将A取走。B离开平台后的落地点与平台右边缘的水平距离
。（取g=10m/s2）求：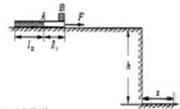
（1）B离开平台时的速度vB。
（2）B从开始运动到刚脱离A时，B运动的时间tB和位移xB。
（3）A左端的长度L2
如图所示，光滑水平面上有一静止小车B，左端固定一砂箱，砂箱的右端连接一水平轻弹簧，小车与砂箱的总质量为M1＝1.99 kg.车上静置一物体A，其质量为M2＝2.00 kg.此时弹簧呈自然长度，物体A的左端的车面是光滑的，而物体A右端的车面与物体间的动摩擦因数为μ＝0.2.现有一质量为m＝0.01 kg的子弹以水平速度v0＝400 m/s打入砂箱且静止在砂箱中，求：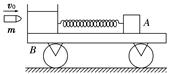
(1)小车在前进过程中，弹簧弹性势能的最大值．
(2)为使物体A不从小车上滑下，车面的粗糙部分至少多长？(g取10 m/s2)
所示，静止放在水平桌面上的纸带，其上有一质量为m＝0．1 kg的铁块，它与纸带右端的距离为L＝0．5 m，铁块与纸带间、纸带与桌面间动摩擦因数均为μ＝0．1．现用力F水平向左将纸带从铁块下抽出，当纸带全部抽出时铁块恰好到达桌面边缘，铁块抛出后落地点离抛出点的水平距离为s＝0．8 m．已知g＝10 m/s2，桌面高度为H＝0．8 m，不计纸带质量，不计铁块大小，铁块不滚动．求：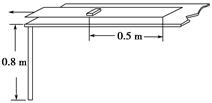
（1）铁块抛出时速度大小；
（2）纸带从铁块下抽出所用时间t1；
（3）纸带抽出过程产生的内能E
如图所示,在水平方向的匀强电场中有一表面光滑、与水平面成45°角的绝缘直杆AC,有一质量500 g的带电小环套在直杆上,正以某一速度,沿杆匀速下滑,小环离开杆下端（C端,距地面高度h="0.8" m）后正好通过C端的正下方P点处.(g取10 m/s2)求：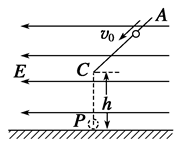
(1)小环离开直杆后运动的加速度大小和方向.
(2)小环从C运动到P点过程中动能的增量.
(3)环在直杆上匀速运动速度的大小v0.