(本小题满分10分)选修4—5:不等式选讲
已知函数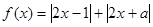 ,
, .
.
(1)当 时,求不等式
时,求不等式 的解集;
的解集;
(2)设 ,且当
,且当 时,
时, ,求
,求 的取值范围.
的取值范围.
已知椭圆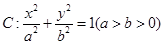 过点
过点 ,且离心率为
,且离心率为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ) 为椭圆
为椭圆 的左、右顶点,直线
的左、右顶点,直线 与
与 轴交于点
轴交于点 ,点
,点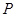 是椭圆
是椭圆 上异于
上异于 的动点,直线
的动点,直线 分别交直线
分别交直线 于
于 两点.证明:
两点.证明: 恒为定值.
恒为定值.
如图,四棱锥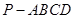 的底面
的底面 是矩形,
是矩形,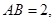
 ,且侧面
,且侧面 是正三角形,平面
是正三角形,平面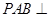 平面
平面 ,
,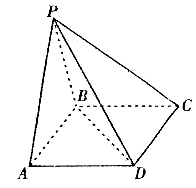
(Ⅰ)求证: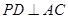 ;
;
(Ⅱ)在棱 上是否存在一点
上是否存在一点 ,使得二面角
,使得二面角 的大小为45°.若存在,试求
的大小为45°.若存在,试求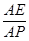 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
某公司向市场投放三种新型产品,经调查发现第一种产品受欢迎的概率为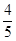 ,第二、第三种产品受欢迎的概率分别为
,第二、第三种产品受欢迎的概率分别为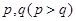 ,且不同种产品是否受欢迎相互独立.记
,且不同种产品是否受欢迎相互独立.记 为公司向市场投放三种新型产品受欢迎的数量,其分布列为
为公司向市场投放三种新型产品受欢迎的数量,其分布列为
 |
0 |
1 |
2 |
3 |
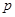 |
 |
 |
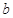 |
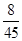 |
(Ⅰ)求 的值
的值
(Ⅱ)求数学期望 .
.
已知△ABC的三个内角A、B、C所对的边分别为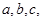 向量
向量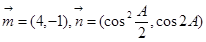 ,且
,且 .
.
(Ⅰ)求角A的大小;
(Ⅱ)若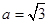 ,试判断
,试判断 取得最大值时△ABC形状.
取得最大值时△ABC形状.
(本小题满分14分)
已知椭圆 的离心率为
的离心率为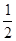 ,点
,点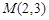 ,
,  为
为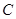 上两点,斜率为
上两点,斜率为 的直线与椭圆
的直线与椭圆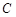 交于点
交于点 ,
,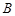 (
( ,
,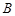 在直线
在直线 两侧).
两侧).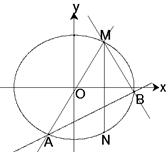
(I)求四边形 面积的最大值;
面积的最大值;
(II)设直线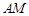 ,
,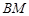 的斜率为
的斜率为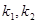 ,试判断
,试判断 是否为定值.若是,求出这个定值;若不是,说明理由.
是否为定值.若是,求出这个定值;若不是,说明理由.