已知:△ABC∽△A′B′C′,AB=4cm,A′B′=10cm,AE是△ABC的一条高,AE=4.8cm.求△A′B′C′中对应高线A′E′的长.
某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本 (单位:元)、销售价
(单位:元)、销售价 (单位:元)与产量x(单位:kg)之间的函数关系.
(单位:元)与产量x(单位:kg)之间的函数关系.
(1)请解释图中点D的横坐标、纵坐标的实际意义;
(2)求线段AB所表示的 与x之间的函数表达式;
与x之间的函数表达式;
(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?
已知一次函数 的图像与
的图像与 轴、
轴、 轴分别相交于点A、B,点P在该函数图像上, P到
轴分别相交于点A、B,点P在该函数图像上, P到 轴、
轴、 轴的距离分别为
轴的距离分别为 、
、 。
。
(1)当P为线段AB的中点时,求 的值;
的值;
(2)直接写出 的范围,并求当
的范围,并求当 时点P的坐标;
时点P的坐标;
(3)若在线段AB 上存在无数个P点,使 (
( 为常数), 求
为常数), 求 的值.
的值.
知识迁移
我们知道,函数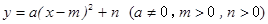 的图像是由二次函数
的图像是由二次函数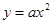 的图像向右平移m个单位,再向上平移n个单位得到.类似地,函数
的图像向右平移m个单位,再向上平移n个单位得到.类似地,函数 的图像是由反比例函数
的图像是由反比例函数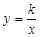 的图像向右平移m个单位,再向上平移n个单位得到,其对称中心坐标为(m,n).
的图像向右平移m个单位,再向上平移n个单位得到,其对称中心坐标为(m,n).
理解应用
函数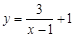 的图像可以由函数
的图像可以由函数 的图像向右平移 个单位,再向上平移 个单位得到,其对称中心坐标为 .
的图像向右平移 个单位,再向上平移 个单位得到,其对称中心坐标为 .
灵活运用
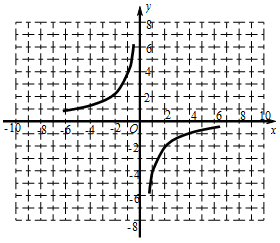
如图,在平面直角坐标系xOy中,请根据所给的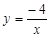 的图像画出函数
的图像画出函数 的图像,并根据该图像指出,当x在什么范围内变化时,
的图像,并根据该图像指出,当x在什么范围内变化时,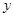 ≥
≥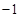 ?
?
实际应用
某老师对一位学生的学习情况进行跟踪研究.假设刚学完新知识时的记忆存留量为1.新知识学习后经过的时间为x,发现该生的记忆存留量随x变化的函数关系为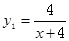 ;若在
;若在 (
(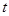 ≥4)时进行一次复习,发现他复习后的记忆存留量是复习前的2倍(复习时间忽略不计),且复习后的记忆存量随x变化的函数关系为
≥4)时进行一次复习,发现他复习后的记忆存留量是复习前的2倍(复习时间忽略不计),且复习后的记忆存量随x变化的函数关系为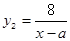 .如果记忆存留量为
.如果记忆存留量为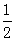 时是复习的“最佳时机点”,且他第一次复习是在“最佳时机点”进行的,那么当x为何值时,是他第二次复习的“最佳时机点”?
时是复习的“最佳时机点”,且他第一次复习是在“最佳时机点”进行的,那么当x为何值时,是他第二次复习的“最佳时机点”?
某工厂以80元/箱的价格购进60箱原材料,准备由甲、乙两车间全部用于生产A产品.甲车间用每箱原材料可生产出A产品12千克,需耗水4吨;乙车间通过节能改造,用每箱原材料可生产出的A产品比甲车间少2千克,但耗水量是甲车间的一半.已知A产品售价为30元/千克,水价为5元/吨.如果要求这两车间生产这批产品的总耗水量不得超过200吨,那么该厂如何分配两车间的生产任务,才能使这次生产所能获取的利润w最大?最大利润是多少?(注:利润=产品总售价-购买原材料成本-水费)
某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本 (单位:元)、销售价
(单位:元)、销售价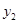 (单位:元)与产量x(单位:kg)之间的函数关系.
(单位:元)与产量x(单位:kg)之间的函数关系.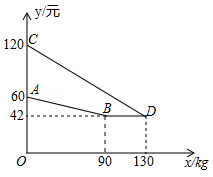
(1)请解释图中点D的横坐标、纵坐标的实际意义;
(2)求线段AB所表示的 与x之间的函数表达式;
与x之间的函数表达式;
(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?