如图,M是直线AB外一点,过点M的直线MN与AB交于点N,过点M画直线CD,使得CD∥AB.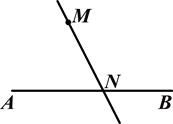
已知两个圆锥的锥角相等,底面面积的比为9:25,其中底面较小的圆锥的底面半径为6cm,求另一个圆锥的底面积的大小.
以斜边长为a的等腰直角三角形的斜边为轴,旋转一周,求所得图形的表面积.
圆锥的高为3cm,底面半径为4cm,求它的侧面积和侧面展开图的圆心角.
已知:如图,AB是⊙O的直径,点C、D为圆上两点,且弧CB=弧CD,CF⊥AB于点F,CE⊥AD的延长线于点E.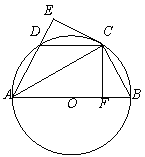
(1)试说明:DE=BF;
(2)若∠DAB=60°,AB=6,求△ACD的面积.
如图1,在平面直角坐标系中,直线AB与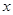 轴交于点A,与
轴交于点A,与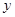 轴交于点B,与直线OC:
轴交于点B,与直线OC: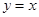 交于点C.
交于点C.

(1)若直线AB解析式为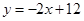 ,
,
①求点C的坐标;
②求△OAC的面积.
(2)如图2,作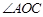 的平分线ON,若AB⊥ON,垂足为E, OA=4,P、Q分别为线段OA、OE上的动点,连结AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.
的平分线ON,若AB⊥ON,垂足为E, OA=4,P、Q分别为线段OA、OE上的动点,连结AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.