在袋子中装有10个大小相同的小球,其中黑球有3个,白球有n(2≤n≤5,且n≠3)个,其余的球为红球.
(Ⅰ)若n=5,从袋中任取1个球,记下颜色后放回,连续取三次,求三次取出的球中恰有2个红球的概率;
(Ⅱ)从袋里任意取出2个球,如果这两个球的颜色相同的概率是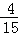 ,求红球的个数;
,求红球的个数;
(Ⅲ)在(Ⅱ)的条件下,从袋里任意取出2个球.若取出1个白球记1分,取出1个黑球记2分,取出1个红球记3分.用ξ表示取出的2个球所得分数的和,写出ξ的分布列,并求ξ的数学期望Eξ.
((本小题满分12分)
数列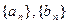 满足:
满足: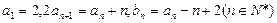
(1)求数列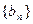 的通项公式;
的通项公式;
(2)设数列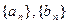 的前n项和分别为An、Bn,问是否存在实数
的前n项和分别为An、Bn,问是否存在实数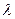 ,使得
,使得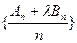 为等差数列?若存在,求出
为等差数列?若存在,求出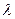 的值;若不存在,说明理由。
的值;若不存在,说明理由。
((本小题满分12分)
一项"过关游戏"规则规定: 在第n 关要抛掷骰子n次, 若这n次抛掷所出现的点数之和大于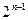 +1 (n∈N*), 则算过关.
+1 (n∈N*), 则算过关.
(1)求在这项游戏中第三关过关的概率是多少?
(2)若规定n≤3, 求某人的过关数ξ的期望.
(本小题满分12分)
如图,在四棱锥P—ABCD中,底面ABCD是正方形,PA⊥平面ABCD,且PA=AB=2,E、F分别为AB、PC的中点。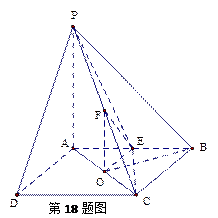
(1)求异面直线PA与BF所成角的正切值。
(2)求证:EF⊥平面PCD。
(本小题满分10分)
已知函数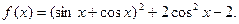
(1)求函数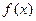 的最小正周期T;
的最小正周期T;
(2)当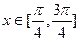 时,求函数
时,求函数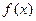 的最大值和最小值。
的最大值和最小值。
如图,直四棱柱 中,底面
中,底面 是
是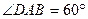
 的菱形,
的菱形,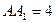 ,
,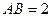 ,点
,点 在棱
在棱 上,点
上,点 是棱
是棱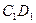 的中点.
的中点.
(1)若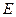 是
是 的中点,求证:
的中点,求证: ;
;
(2)求出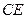 的长度,使得
的长度,使得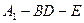 为直二面角.
为直二面角.