从甲、乙、丙三人中选取2人去参加运动会有甲和乙、甲和丙、乙和丙3种不同的选法．抽象成数学模型，即：从3个元素中选取2个元素的组合，记作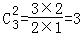
；一般地，从m个元素中选取n个元素（n≤m）的组合，记作
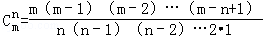．根据以上分析从8人中选取5人去参加运动会的不同选法有 种．
如图，若双曲线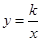
与边长为5的等边△AOB的边OA、AB分别相交于C、D两点，且OC＝3BD，则实数k的值为________．
在Rt△ABC中，CA＝CB，
，点D在BC边上，连接AD，若
，则BD的长为________．
如图，在直角三角形ABC（∠C＝90°）中，放置边长分别为3，4，x的三个正方形，则x的值为________．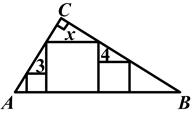
如图，直线x＝2与反比例函数
，
的图象分别交于A，B两点，若点P是y轴上任意一点，则△PAB的面积是________．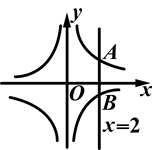
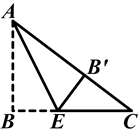
如图，在Rt△ABC中，∠B＝90°，AB＝3，BC＝4，将△ABC折叠，使点B恰好落在斜边AC上，与点B′重合，AE为折痕，则EB′＝________．