如图，已知点B、D、E、C在同一直线上，AB=AC，AD=AE．
求证：BD=CE
（1）根据下面说理步骤填空
证法一：作AM⊥BC，垂足为M．
∵AB=AC（ ） AM⊥BC（ 辅助线 ）
∴BM=CM（ ）
同理DM=EM．
∴BM﹣DM=CM﹣EM（ ）
∴BD=CE（线段和、差的意义）
（2）根据下面证法二的辅助线完成后面的说理步骤．
证法二：作△ABC的中线AM．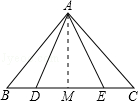
解不等式组：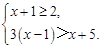
如图1，关于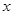
的二次函数y=－
+bx+c经过点A（－3,0），点C（0,3），点D为二次函数的顶点，DE为二次函数的对称轴，E在x轴上。
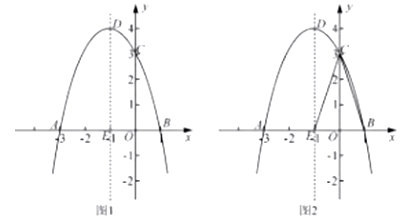
（1）求抛物线的解析式；
（2）DE上是否存在点P到AD的距离与到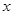轴的距离相等，若存在求出点P，若不存在请说明理由；
（3）如图2，DE的左侧抛物线上是否存在点F，使2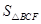
=3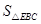
，若存在求出点F的坐标，若不存在请说明理由。
如图1，水平放置一个三角板和一个量角器，三角板的边AB和量角器的直径DE在一条直线上，AB=BC=6cm，OD=3cm开始的时候BD=1cm,现在三角板以2cm/s的速度向右移动。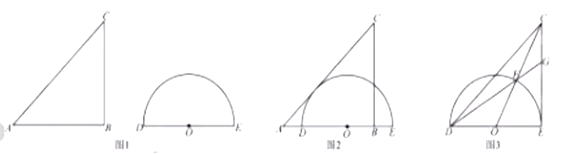
（1）当B与O重合的时候，求三角板运动的时间；
（2）如图2，当AC与半圆相切时，求AD；
（3）如图3，当AB和DE重合时，求证：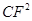
=CG·CE.
下表为深圳市居民每月用水收费标准，（单位：元/m3）。
| 用水量 |
单价 |
| x≤22 |
a |
| 剩余部分 |
a+1.1 |
（1）某用户用水10立方米，公交水费23元，求a的值；
（2）在（1）的前提下，该用户5月份交水费71元，请问该用户用水多少立方米？
小丽为了测旗杆AB的高度，小丽眼睛距地图1.5米，小丽站在C点，测出旗杆A的仰角为30o，小丽向前走了10米到达点E，此时的仰角为60o，求旗杆的高度。