阅读下面的文字,解答问题.
大家知道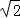 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此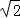 的小数部分我们不可能全部地写出来,但是由于1<
的小数部分我们不可能全部地写出来,但是由于1<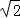 <2,所以
<2,所以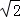 的整数部分为1,将
的整数部分为1,将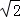 减去其整数部分1,差就是小数部分
减去其整数部分1,差就是小数部分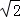 ﹣1,根据以上的内容,解答下面的问题:
﹣1,根据以上的内容,解答下面的问题:
(1)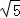 的整数部分是 ,小数部分是 ;
的整数部分是 ,小数部分是 ;
(2)1+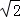 的整数部分是 ,小数部分是 ;
的整数部分是 ,小数部分是 ;
(3)若设2+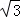 整数部分是x,小数部分是y,求x﹣
整数部分是x,小数部分是y,求x﹣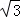 y的值.
y的值.
某公司有 型产品40件,
型产品40件, 型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
 型利润 型利润 |
 型利润 型利润 |
|
| 甲店 |
200 |
170 |
| 乙店 |
160 |
150 |
(1)设分配给甲店 型产品
型产品 件,这家公司卖出这100件产品的总利润为
件,这家公司卖出这100件产品的总利润为 (元),求
(元),求 关于
关于 的函数关系式,并求出
的函数关系式,并求出 的取值范围;
的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来;
(3)为了促销,公司决定仅对甲店 型产品让利销售,每件让利
型产品让利销售,每件让利 元,但让利后
元,但让利后 型产品的每件利润仍高于甲店
型产品的每件利润仍高于甲店 型产品的每件利润.甲店的
型产品的每件利润.甲店的 型产品以及乙店的
型产品以及乙店的 型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
如图,BD为⊙O的直径,AB=AC, AD交BC于点E,AE=2,ED=4,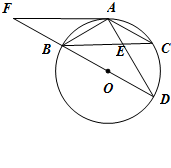
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
“知识改变命运,科技繁荣祖国”.我市中小学每年都要举办一届科技比赛.下图为我市某校2011年参加科技比赛(包括电子百拼、航模、机器人、建模四个类别)的参赛人数统计图:
(1)该校参加机器人、建模比赛的人数分别是人和人;
(2)该校参加科技比赛的总人数是人,电子百拼所在扇形的圆心角的度数是°,并把条形统计图补充完整;
(3)从全市中小学参加科技比赛选手中随机抽取80人,其中有32人获奖. 今年我市
中小学参加科技比赛人数共有2485人,请你估算今年参加科技比赛的获奖人数约是多少人?
如图所示,每一个小方格都是边长为1的单位正方形。△ABC的三个顶点都在格点上,以点O为坐标原点建立平面直角坐标系。
(1)画出△ABC先向左平移3个单位,再向下平移2个单位的△A1B1C1,并写出点B1的坐标;
(2)画出将△ABC绕点O顺时针旋转90°后的△A2B2C2,并求出点A旋转到A2所经过的路径长。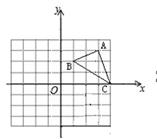
已知关于 的函数
的函数 的图像与坐标轴只有2个交点,求
的图像与坐标轴只有2个交点,求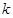 的值.
的值.