如图．已知由平行四边形ABCD各顶点向形外一条直线l作垂线，设垂足分别为A′，B′，C′，D′．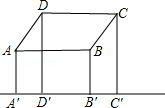
（1）求证：A′A+C′C=B′B+D′D；
（2）如果移动直线l，使它与四边形ABCD的位置关系相对变动得更特殊一些（如l过A，或l交AB，BC等），那么，相应地结论会有什么变化？试作出你的猜想和证明；
（3）如果考虑直线l和平行四边形更一般的关系（如平行四边形变成圆，或某一中心对称图形，垂线AA'，BB'，CC'，DD'只保持平行等），那么又有什么结论，试作出你的猜想和证明．
如图，在□ABCD中，E、F为BC上的两点，且BE=CF，AF=DE．
求证：（1）△ABF≌△DCE；
（2）四边形ABCD是矩形．
解方程：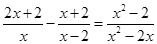
计算
（1）
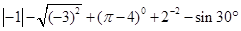
（2）
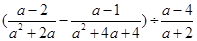，其中a满足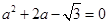
如图1所示，将一个边长为2的正方形
和一个长为2、宽为1的长方形
拼在一起，构成一个大的长方形
．现将小长方形绕点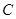
顺时针旋转至
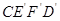，旋转角为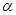
．
（1）当点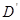
恰好落在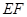
边上时，求旋转角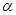的值；
（2）如图2，
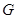为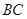
的中点，且0°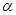＜＜90°，求证：
；
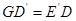（3）先将小长方形绕点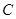顺时针旋转，使
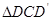与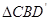
全等（0°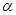＜＜180°)，再将此时的小长方形
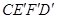沿CD边竖直向上平移t个单位，设移动后小长方形边直线
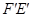与BC交于点H，若DH∥FC，求上述运动变换过程中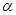和t的值．
函数
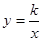和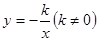
的图象关于y轴对称，我们定义函数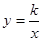和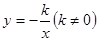相互为“影像”函数。
类似地，如果函数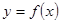
和
的图象关于y轴对称，那么我们定义函数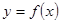和互为“影像”函数。
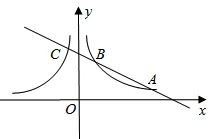
（1）请写出函数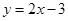
的“影像”函数：；
（2）函数的“影像”函数是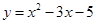
；
（3）如果，一条直线与一对“影像”函数
和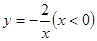
的图象分别交于点A、B、C（点A、B在第一象限），如果CB: BA=1:2，点C在函数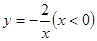的“影像”函数上的对应点的横坐标是1，求点B的坐标。