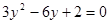如图,把长方形纸片ABCD沿EF折叠,使得点D与点B重合,点C落在点C′的位置上.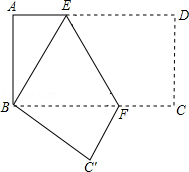
(1)试说明△BEF是等腰三角形;
(2)图形中是否存在成中心对称的两个图形?如果存在,请指出是哪两个图形(不必说明理由,图中实线、虚线一样看待);
(3)若AB=4,AD=8,求折痕EF的长度.
在 中,
中, ,点P从点A开始沿AB边向点B以
,点P从点A开始沿AB边向点B以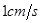 的速度移动,点Q从点B沿BC向点C以
的速度移动,点Q从点B沿BC向点C以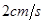 的速度移动.如果点P、Q分别从A、B同时出发.
的速度移动.如果点P、Q分别从A、B同时出发.
(1)几秒后, 的面积等于
的面积等于 ;
;
(2)经过几秒后,PQ之间的距离为 ;
;
(3)在P、Q两点的运动过程中, 可能是等腰三角形吗?请说明理由.
可能是等腰三角形吗?请说明理由.
某超市经销一种成本 的产品.市场调查发现,按
的产品.市场调查发现,按 销售,一个月能销售出500千克.销售每涨1元,月销售量就减少10千克.针对这种产品的销售情况,超市在月成本不超过10000元的情况下,使得月销售利润达到8000元.问销售单位应定为多少元?销售量为多少?
销售,一个月能销售出500千克.销售每涨1元,月销售量就减少10千克.针对这种产品的销售情况,超市在月成本不超过10000元的情况下,使得月销售利润达到8000元.问销售单位应定为多少元?销售量为多少?
关于x的方程 有两个不相等的实数根.
有两个不相等的实数根.
(1)求k的取值范围;
(2)是否存在实数k,使方程的两个实数根的倒数和等于0?若存在,求出k的值;若不存在,请说明理由.
如图,在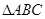 中,
中,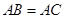 ,
,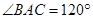 ,
,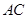 的垂直平分线
的垂直平分线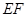 交
交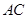 于点
于点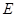 ,交
,交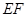 于点
于点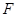 ,
,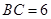 .求
.求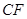 的长.
的长.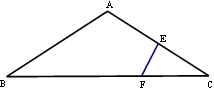
解方程:
(1)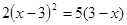 (2)
(2)
(3)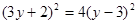 (4)
(4)