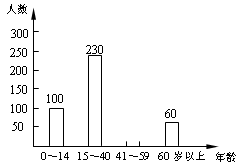
小明学完统计知识后,随机调查了他所住小区若干名居民的年龄,将调查数据绘制成如下扇形和条形统计图: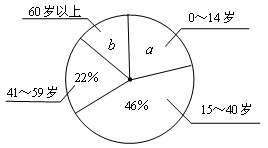
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)小明共调查了 名居民的年龄,扇形统计图中a= ,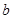 = ;
= ;
(2)补全条形统计图;
(3)若该辖区年龄在0~14岁的居民约有3500人,请估计年龄在15~59岁的居民的人数.
解方程:x2+7x+12=0。
如图,把一副三角板如图(1)放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=4,CD=5。把三角板DCE绕着点C顺时针旋转15°得到△D1CE1(如图2),此时AB与CD1交于点O,则线段AD1的长度为。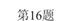

如图,已知四边形ABCD中,∠C=∠D=90°,AE平分∠DAB,BE平分∠ABC,且E在D上.
(1)求∠AEB;
(2)求证:DE=CE.
如图,将长方形ABCD沿直线BD折叠,使点C落在点C′处,BC′交AD于E,AD=8,AB=4.求△BED 的面积.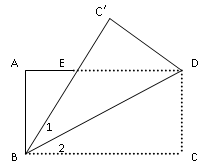
天水一家饮料公司将一种新研发的饮料免费送给一些人品尝,并让每个人按A(不喜欢)、B(一般)、C(比较喜欢)、D(非常喜欢)四个等级对该饮料进行评价,图①和图②是该公司采集数据后,绘制的两幅不完整的统计图.
请你根据以上统计图提供的信息,回答下列问题:
(1)本次调查的人数为________人;
(2)图①中,a=________,C等级所占的圆心角的度数为________度;
(3)请直接在上图中补全条形统计图.