如图所示,Ⅰ、Ⅱ、Ⅲ为电场和磁场的理想边界,一束电子(电量为e,质量为m,重力不计)由静止状态从P点经过Ⅰ、Ⅱ间的电场加速后垂直到达边界Ⅱ的Q点。匀强磁场的磁感应强度为B,磁场边界宽度为d,电子从磁场边界Ⅲ穿出时的速度方向与电子原来的入射方向夹角为30°。求: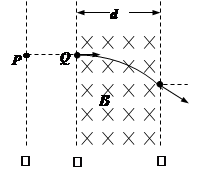
(1)电子在磁场中运动的时间t;
(2)若改变PQ间的电势差,使电子刚好不能从边界Ⅲ射出,则此时PQ间的电势差U是多少?
(18分)如图甲所示,直角坐标系中直线AB与横轴x夹角∠BAO=30°,AO长为a。假设在点A处有一放射源可沿∠BAO所夹范围内的各个方向放射出质量为m、速度大小均为 、带电量为e的电子,电子重力忽略不计。在三角形ABO内有垂直纸面向里的匀强磁场,当电子从顶点A沿AB方向射入磁场时,电子恰好从O点射出。试求:
、带电量为e的电子,电子重力忽略不计。在三角形ABO内有垂直纸面向里的匀强磁场,当电子从顶点A沿AB方向射入磁场时,电子恰好从O点射出。试求: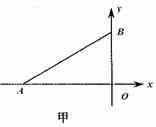
(1)从顶点A沿AB方向射入的电子在磁场中的运动时间t;
(2)速度大小为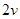 的电子从顶点A沿AB方向射入磁场(其它条件不变),求从磁场射出的位置坐标。
的电子从顶点A沿AB方向射入磁场(其它条件不变),求从磁场射出的位置坐标。
(3)磁场大小、方向保持不变,改变匀强磁场分布区域,使磁场存在于三角形ABO内的左侧,要使放射出的速度大小为 电子穿过磁场后都垂直穿过y轴后向右运动,试求匀强磁场区域分布的最小面积S。(用阴影表示最小面积)
电子穿过磁场后都垂直穿过y轴后向右运动,试求匀强磁场区域分布的最小面积S。(用阴影表示最小面积)
特警队员从悬停在空中离地235米高的直升机上沿绳下滑进行降落训练,某特警队员和他携带的武器质量共为80 kg,设特警队员用特制的手套轻握绳子时可获得200 N的摩擦阻力,紧握绳子时可获得1000 N的摩擦阻力,下滑过程中特警队员不能自由落体,至少轻握绳子才能确保安全。g取10m/s2. 求:
(1)特警队员轻握绳子降落时的加速度是多大?
(2)如果要求特警队员在空中下滑过程中先轻握绳子加速下降,再紧握绳子减速下降,且着地时的速度等于5m/s,则下落时间是多少?
如图甲所示,空间存在B=0.5T,方向竖直向下的匀强磁场,MN、PQ是处于同一水平面内相互平行的粗糙长直导轨,间距L=0.2m, R是连接在导轨一端的电阻,ab是跨接在导轨上质量为m=0.1kg的导体棒。从零时刻开始,通过一小型电动机对ab棒施加一个牵引力F,方向水平向左,使其从静止开始沿导轨做加速运动,此过程中棒始终保持与导轨垂直且接触良好。图乙是棒的v-t图象,其中OA段是直线,AC是曲线,DE是曲线图象的渐进线,小型电动机在12s末达到额定功率P=4.5W,此后保持功率不变。除R外,其余部分电阻均不计,g=10m/s2。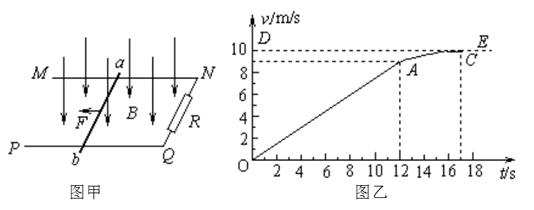
(1)求导体棒ab在0-12s内的加速度大小
(2)求导体棒ab与导轨间的动摩擦因数及电阻R的值
(3)若t=17s时,导体棒ab达最大速度,从0-17s内共发生位移100m,试求12s-17s内,R上产生的热量是多少?
在一广阔的匀强磁场中,建立一直角坐标系,如图所示,在坐标系的原点O释放一速率为v,质量为m电荷量为十q的粒子(重力不计),释放时速度方向垂直于B的方向,且与x轴成30°角,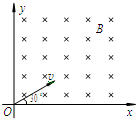
则(1)其第一次经过y轴时,轨迹与y轴交点离O点距离为多少?(不考虑空气阻力)
(2粒子从O点开始运动到穿过y轴时所用的时间
(3粒子做圆周运动圆心的坐标
如图所示,面积为0.2m2的100匝线圈A处在磁场中,磁场方向垂直于线圈平面.磁感强度随时间变化的规律是B=(6-0.2t) (T)已知R1=4Ω,R2=6Ω,电容C=30μF,线圈A的电阻不计.求:
(1)闭合S后,通过R2的电流强度大小和方向。
(2)闭合S一段时间后在断开S,S断开后通过R2的电荷量是多少?