心理学家研究发现,一般情况下,学生的注意力随着教师讲课时间的变化而变化,讲课开始时学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的状态,随后学生的注意力开始分散,经过实验分析可知,一般地,学生的注意力y随时间t的变化情况如下表:
| 上课时间t |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
| 学生的注意力y |
100 |
191 |
240 |
240 |
240 |
205 |
170 |
135 |
100 |
65 |
(1)讲课开始后第5分钟时与讲课开始后第25分钟时比较,何时学生的注意力更集中?
(2)从表中观察,讲课开始后,学生的注意力最集中的时间是那一段?
(3)从表中观察,讲课开始后,学生的注意力从第几分钟起开始下降?猜想注意力下降过程中y与t的关系,并用式子表示出来。
用(3)题中的关系式,求当t=27分时,学生的注意力y的值是多少。现有一道数学难题,需要讲解20分钟,为了效果更好,要求学生的注意力最低达到190,那么老师能否在学生注意力达到所需状态下讲完这道题目,试着说明理由。
在3×3的正方形格点图中,有格点△ABC和△DEF,且△ABC和△DEF关于某直线成轴对称,请在下面给出的图中画出4个这样的△DEF.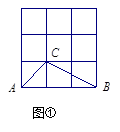


如图,点B、E、C、F在同一条直线上,∠A=∠D,∠B=∠DEF,BE=CF.
求证:AC=DF
如图△ABC,用圆规和直尺再画一个△DEF,使△DEF≌△ABC.
如图,点D在AB上,点E在AC上,AB=AC,AD=AE.
求证:∠B=∠C.
(本题10分)如图,已知△ABC中,AB=AC=6cm,∠B=∠C,BC=4cm,点D为AB的中点.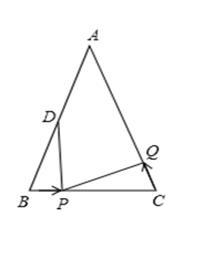
(1)如果点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,则经过 秒后,点P与点Q第一次在△ABC的AC边上相遇?(在横线上直接写出答案,不必书写解题过程)