阅读下面材料: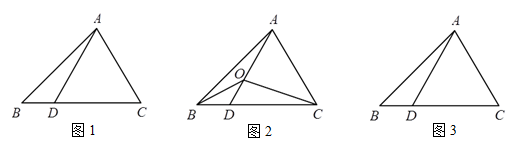
如图1,在△ABC中,D是BC边上的点(不与点B、C重合),连结AD.
(1)当点D是BC边上的中点时,S△ABD:S△ABC= ;
(2)如图2,在△ABC中,点O是线段AD上一点(不与点A、D重合),且AD=nOD,连结BO、CO,求S△BOC:S△ABC的值(用含n的代数式表示);
(3)如图3,O是线段AD上一点(不与点A、D重合),连结BO并延长交AC于点F,连结CO并延长交AB于点E,补全图形并直接写出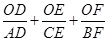 的值.
的值.
已知:关于x的一元二次方程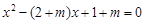
(1)求证:方程有两个实数根;
(2)设m<0,且方程的两个实数根分别为
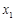 ,
,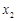 (其中
(其中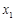 <
<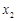 ),若y是关于m的函数,且
),若y是关于m的函数,且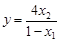 ,求这个函数的解析式;
,求这个函数的解析式;(3)在(2)的条件下,利用函数图象求关于m的方程
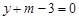 的解。
的解。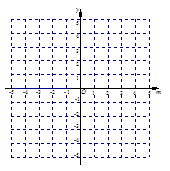
如图,在△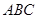 中,
中,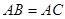 ,以
,以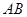 为直径的⊙O分别交
为直径的⊙O分别交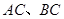 于点
于点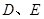 , 点
, 点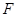 在
在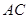 的延长线上,且
的延长线上,且 ∠
∠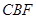
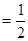 ∠
∠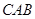 。
。
(1) 求证:AB⊥BF
(2) 若
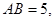 sin∠CBF=
sin∠CBF=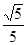 ,求BC和BF的长。
,求BC和BF的长。
某商场经销一种高档水果,如果每千克盈利10元,每天可出售500千克,经调查发现在进价不变的情况下,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,同时又要顾客得到实惠,那么每千克应涨价多少元?
已知,如图,D是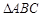 中BC边的中点,
中BC边的中点,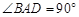 ,
,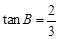 , AD=2
, AD=2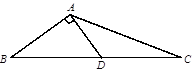
求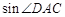 ;
;
AC的长及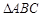 的面积。
的面积。
如图,已知点C、D在以O为圆心,AB为直径的半圆上,且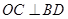 于点M,CF⊥AB于点F交BD于点E,
于点M,CF⊥AB于点F交BD于点E,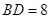 ,
,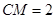
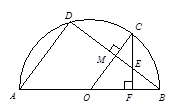
(1)求⊙O的半径;
(2)求证:CE = BE.