方格纸中的每个小方格都是边长为1的正方形，我们把以格点间连线为边的三角形称为“格点三角形”．图中的△ABC是格点三角形．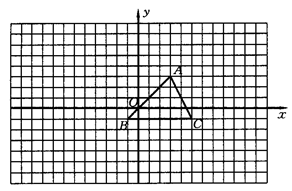
（1）把△ABC关于y轴对称后得到△A1B1C1，画出△A1B1C1的图形。
（2）把△ABC以点A为位似中心放大，使放大前后对应边长的比为1：2，画出△A B2C2的图形．
小数3．575757是循环小数． （）
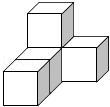
用小立方块搭一个几何体，使它从正面和上面看到的形状如图所示，从上面看到形状中小正方形中的字母表示在该位置上小立方块的个数，请问：
（1）
，
各表示几？ 答：
_____ ，
_____；
（2）这个几何体最少由_____个小立方块搭成，最多由____个小立方块搭成；
（3）能搭出满足条件的几何体共有____种情况，其中从左面看这个几何体的形状图共有____种，请在所给网格图中画出其中的任意一种．
佛山市客运管理部门对“十一”国庆假期七天的客流变化量进行了不完全统计，
数据如下表（用正数表示客流量比前一天上升数，用负数表示下降数）：
| 日期 |
1日 |
2日 |
3日 |
4日 |
5日 |
6日 |
7日 |
| 变化/万人 |
10 |
-3 |
-5 |
-1 |
2 |
5 |
3 |
（1）国庆期间，10月_____日的客流量最低；（直接写出日期）
（2）与9月30日相比，10月7日的客流量是上升了还是下降了？变化了多少？
矿井下A，B，C三处的高度分别是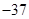
，
，
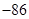
，A处比B处高多少米？C处比B处低多少米？
如题20图是由几个小正方体堆成的几何体，请在所给的网格图中分别画出从正面、
从上面看到这个几何体的形状图．
