如图,等腰△OAB在直角坐标系中的位置如图,点A的坐标为( ,3),点B的坐标为(-6,0).
,3),点B的坐标为(-6,0).
(1)若△OAB关于y轴的轴对称图形是三角形OA′B′,请直接写出A、B的对称点A′、B′的坐标;
(2)若将三角形OAB沿x轴向右平移a个单位,此时点A恰好落在反比例函数 的图像上,求a的值;
的图像上,求a的值;
(3)若△OAB绕点O按逆时针方向旋转α度(0<α<90).
①当α=30°时点B恰好落在反比例函数 的图象上,求k的值;
的图象上,求k的值;
②问点A、B能否同时落在①中的反比例函数的图象上,若能,求出α的值;若不能,请说明理由.
已知直线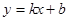 经过点(1,2)和点(
经过点(1,2)和点( ,4),求这条直线的解析式.
,4),求这条直线的解析式.
(本小题满分12分)
已知二次函数图象的顶点坐标为M(1,0),直线 与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在
与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在 轴上.
轴上.
(1)求m的值及这个二次函数的解析式;
(2)若P(
 ,0) 是
,0) 是 轴上的一个动点,过P作
轴上的一个动点,过P作 轴的垂线分别与直线AB和二次函数的图象交于D、E两点.
轴的垂线分别与直线AB和二次函数的图象交于D、E两点.
①当0< < 3时,求线段DE的最大值;
< 3时,求线段DE的最大值;
②若直线AB与抛物线的对称轴交点为N,
问是否存在一点P,使以M、N、D、E
为顶点的四边形是平行四边形?若存在,
请求出此时P点的坐标;若不存在,请
说明理由.
(本小题满分10分)
如图,AB是⊙O的直径,弦DE垂直平分半径OA,垂足为C,弦DF与半径OB相交于点P.连结EF,EO .若DE= ,∠DPA=45°
,∠DPA=45°
(1)求⊙O的半径;
(2)求图中阴影部分的面积.(结果保留两个有效数字)
(本小题满分10分)
设函数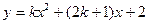 (
( 为任意实数)
为任意实数)(1)求证:不论
 为何值,该函数图象都过点(0,2)和(-2,0);
为何值,该函数图象都过点(0,2)和(-2,0);(2)若该函数图象与
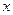 轴只有一个交点,求
轴只有一个交点,求 的值.
的值.
(本小题满分8分)
已知:如图,在⊙O中,AB=CD.
求证:∠ABD=∠CDB