(本小题满分13分)在四棱锥 中,底面
中,底面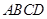 是正方形,
是正方形,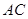 与
与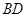 交于点
交于点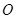 ,
,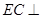 底面
底面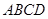 ,
,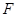 为
为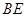 的中点.
的中点. 
(Ⅰ)求证: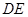 ∥平面
∥平面 ;
;
(Ⅱ)求证: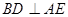 ;
;
(Ⅲ)若 在线段
在线段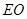 上是否存在点
上是否存在点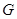 ,使
,使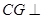 平面
平面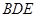 ?
?
若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
(本小题满分12分)
已知函数 ,a∈R
,a∈R
(1)若a =2,求函数 的单调区间;,
的单调区间;,
(2)若a =0,求证: ,
, 恒成立.
恒成立.
(本小题满分12分)
已知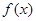 是R上的单调函数,且"x∈R,
是R上的单调函数,且"x∈R,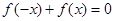 ,若
,若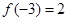
(1) 试判断函数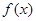 在R上的增减性,并说明理由
在R上的增减性,并说明理由
(2) 解关于x的不等式 ,其中m∈R且m > 0
,其中m∈R且m > 0
(本小题满分12分)
已知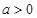 且a≠1,数列
且a≠1,数列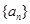 中,
中,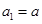 ,
, (
(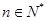 ),令
),令
(1)若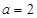 ,求数列
,求数列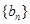 的前n项和Sn;
的前n项和Sn;
(2) 若 ,
,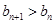 ,n∈N*,求a的取值范围
,n∈N*,求a的取值范围
(本小题满分12分)
已知 ,
, (ω>0),函数
(ω>0),函数 的最小正周期为π
的最小正周期为π
(1) 求函数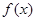 的单调递减区间及对称中心;
的单调递减区间及对称中心;
(2) 求函数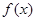 在区间
在区间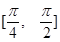 上的最大值与最小值.
上的最大值与最小值.
(本小题满分12分)
已知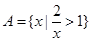 ,
,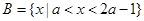 ,a∈R,若“x∈A”是“x∈B”的必要条件,求a的取值范围
,a∈R,若“x∈A”是“x∈B”的必要条件,求a的取值范围