(本小题满分14分)已知函数 .
.
(Ⅰ)若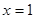 时,
时,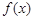 取得极值,求
取得极值,求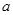 的值;
的值;
(Ⅱ)求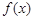 在
在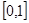 上的最小值;
上的最小值;
(Ⅲ)若对任意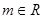 ,直线
,直线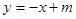 都不是曲线
都不是曲线 的切线,求
的切线,求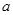 的取值范围.
的取值范围.
已知点P在曲线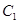 :
: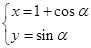 (
(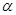 为参数,
为参数,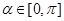 )上,点Q在曲线
)上,点Q在曲线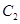 :
: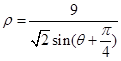 上
上
(1)求曲线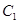 的普通方程和曲线
的普通方程和曲线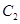 的直角坐标方程;
的直角坐标方程;
(2)求点P与点Q之间距离的最小值.
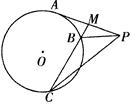
自圆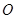 外一点
外一点 引圆的一条切线
引圆的一条切线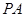 ,切点为
,切点为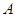 ,
,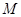 为
为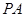 的中点,过点
的中点,过点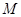 引圆
引圆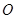 的割线交该圆于
的割线交该圆于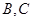 两点,且
两点,且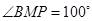 ,
,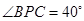 .
.
⑴求证: 与
与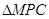 相似;
相似;
⑵求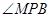 的大小.
的大小.
已知函数 ,其中
,其中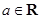 .
.
(Ⅰ)求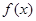 的单调区间;
的单调区间;
(Ⅱ)若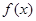 在
在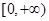 上存在最大值和最小值,求
上存在最大值和最小值,求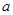 的取值范围.
的取值范围.
已知抛物线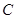 :
: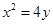 ,过点
,过点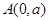 (其中
(其中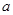 为正常数)任意作一条直线
为正常数)任意作一条直线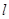 交抛物线
交抛物线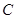 于
于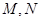 两点,
两点,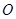 为坐标原点.
为坐标原点.
(1)求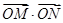 的值;
的值;
(2)过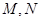 分别作抛物线
分别作抛物线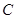 的切线
的切线 ,试探求
,试探求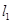 与
与 的交点是否在定直线上,证明你的结论.
的交点是否在定直线上,证明你的结论.
如图,在斜三棱柱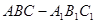 中,点
中,点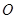 、
、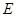 分别是
分别是 、
、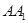 的中点,
的中点, 平面
平面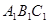 .已知
.已知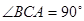 ,
,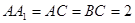 .
.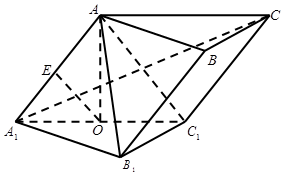
(Ⅰ)证明: 平面
平面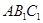 ;
;
(Ⅱ)求异面直线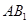 与
与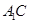 所成的角;
所成的角;
(Ⅲ)求 与平面
与平面 所成角的正弦值.
所成角的正弦值.