甲、乙两个样本的相关信息如下:
样本甲数据:1,6,2,3;
样本乙方差:S2乙=3.4.
(1)计算样本甲的方差; (2)试判断哪个样本波动大.
某市把中学生学习情绪的自我控制能力分为四个等级,即A级:自我控制能力很强;B级;自我控制能力较好;C级:自我控制能力一般;D级:自我控制能力较差。通过对
该市农村中学的初中学生学习情绪的自我控制能力的随机抽样调查,得到下面两幅不完整
的统计图,请根据图中的信息解决下面的问题。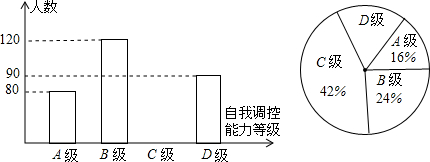
(1)在这次随机抽样调查中,共抽查了多少名学生?
(2)求自我控制能力为C级的学生人数;
(3)求扇形统计图中D级所占的圆心角的度数;
(4)请你估计该市农村中学60000名初中学生中,学习情绪自我控制能力达B级及以上等级的人数是多少?
某工厂生产A、B两种产品共50件,其生产成本与利润如下表:
| A种产品 |
B种产品 |
|
| 成本 (万元/件) |
0.6 |
0.9 |
| 利润 (万元/件) |
0.2 |
0.4 |
若该工厂计划投入资金不超过40万元,且希望获利超过16万元,问工厂有哪几种生产方案?哪种生产方案获利润最大?最大利润是多少?
如图,一天,我国一渔政船航行到A处时,发现正东方向的我领海区域B处有一可疑渔船,正在以12海里∕小时的速度向西北方向航行,我渔政船立即沿北偏东60º方向航行,1.5小时后,在我领海区域的C处截获可疑渔船。问我渔政船的航行路程是多少海里?(结果保留根号)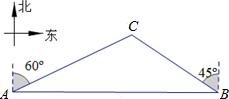
在一个不透明的口袋中装有3个带号码的球,球号分别为2,3,4,这些球除号码不同外其它均相同。甲、乙、两同学玩摸球游戏,游戏规则如下:
先由甲同学从中随机摸出一球,记下球号,并放回搅匀,再由乙同学从中随机摸出一球,记下球号。将甲同学摸出的球号作为一个两位数的十位上的数,乙同学的作为个位上的数。若该两位数能被4整除,则甲胜,否则乙胜.
问:这个游戏公平吗?请说明理由。
如图,抛物线 与x轴交于C.A两点,与y轴交于点B,OB=4.点O关于直线AB的对称点为D,E为线段AB的中点.
与x轴交于C.A两点,与y轴交于点B,OB=4.点O关于直线AB的对称点为D,E为线段AB的中点.
(1)分别求出点A.点B的坐标;
(2)求直线AB的解析式;
(3)若反比例函数 的图象过点D,求k值;
的图象过点D,求k值;
(4)两动点P、Q同时从点A出发,分别沿AB.AO方向向B.O移动,点P每秒移动1个单位,点Q每秒移动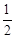 个单位,设△POQ的面积为S,移动时间为t,问:S是否存在最大值?若存在,求出这个最大值,并求出此时的t值;若不存在,请说明理由.
个单位,设△POQ的面积为S,移动时间为t,问:S是否存在最大值?若存在,求出这个最大值,并求出此时的t值;若不存在,请说明理由.