将油箱注满k升油后，轿车可行驶的总路程S（单位：千米）与平均耗油量a（单位：升/千米）之间是反比例函数关系S=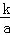
（k是常数，k≠0）．已知某轿车油箱注满油后，以平均耗油量为每千米耗油0.1升的速度行驶，可行驶700千米．
（1）求该轿车可行驶的总路程S与平均耗油量a之间的函数解析式（关系式）；
（2）当平均耗油量为0.08升/千米时，该轿车可以行驶多少千米？
如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（2，﹣1）、B（1，﹣4）、C（3，﹣2）．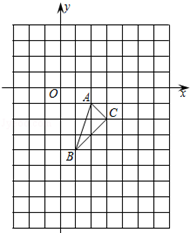
（1）△ABC绕原点O逆时针旋转90°，画出旋转后得到的△A1B1C1，并求边AC在旋转过程中扫过的图形面积；
（2）以原点O为位似中心，位似比为1：2，在y轴的右侧，画出△ABC放大后的图形△A2B2C2．如果点D（a，b）在线段AB上，那么请直接写出点D的对应点D2的坐标．
（1）计算：
﹣2sin60°+｜-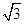
｜；
（2）解方程：x2+4x﹣1=0．
每年的6月5日为世界环保日，为提倡低碳环保，某公司决定购买10台节省能源的新机器，现有甲、乙两种型号的新机器可选，其中每台的价格、工作量如下表．
| 甲型机器 |
乙型机器 |
|
| 价格（万元/台） |
a |
b |
| 产量（吨/月） |
240 |
180 |
经调查：购买一台甲型机器比购买一台乙型机器多2万元，购买2台甲型机器比购买3台乙型机器少6万元．
（1）求a、b的值；
（2）若该公司购买新机器的资金不能超过110万元，请问该公司有几种购买方案？
（3）在（2）的条件下，若公司要求每月的产量不低于2040吨，请你为该公司设计一种最省钱的购买方案．
如图，在平面直角坐标系中，长方形ABCD的边BC∥x轴，如果A点坐标是（﹣1，2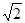
），C点坐标是（3，﹣2）．
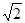（1）直接写出B点和D点的坐标B（）；D（）．
（2）将这个长方形先向右平移1个单位长度长度，再向下平移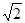个单位长度，得到长方形A1B1C1D1，请你写出平移后四个顶点的坐标；
（3）如果Q点以每秒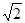个单位长度的速度在长方形ABCD的边上从A出到到C点停止，沿着A﹣D﹣C的路径运动，那么当Q点的运动时间分别是1秒，4秒时，△BCQ的面积各是多少？请你分别求出来．
某学校为了学生的身体健康，每天开展体育活动一小时，开设排球、篮球、羽毛球、体操四项体育活动课．学生可根据自己的爱好任选其中一项，老师根据学生报名情况进行了统计，并绘制了下面尚未完成的扇形统计图和频数分布直方图，请你结合图中的信息，解答下列问题：
（1）该校学生报名总人数有多少人？
（2）从表中可知选羽毛球的学生有多少人？选排球和篮球的人数分别占报名总人数的百分之几？
（3）频数分布直方图补充完整．