杂技团进行杂技表演，演员从跷跷板右端A处弹跳到人梯顶端椅子B处，其身体（看成一个点）的路线是抛物线y＝－
x2＋3x＋1的一部分.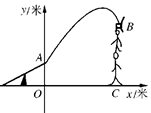
（1）求演员弹跳离地面的最大高度；
（2）已知人梯高BC＝3.4米，在一次表演中，人梯到起跳点A的水平距离是4米，问这次表演是否成功？说明理由．
因式分解：
（1）
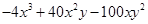
（2）
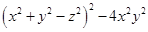
如图，在△ABC中，BA=BC，D在边CB上，且DB=DA=AC．
（1）如图1，填空∠B= °，∠C= °；
（2）若M为线段BC上的点，过M作直线MH⊥AD于H，分别交直线AB、AC与点N、E，如图2
①求证：△ANE是等腰三角形；
②试写出线段BN、CE、CD之间的数量关系，并加以证明．
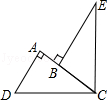
如图，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于E，AD⊥CE于D．
（1）求证：△ADC≌△CEB．
（2）AD=5cm，DE=3cm，求BE的长度．
如图所示，已知点A，F，E，C在同一直线上，AB∥CD，∠ABE=∠CDF，AF=CE．
（1）从图中任找两组全等三角形；
（2）从（1）中任选一组进行证明．
如图，∠DCE=90°，CD=CE，AD⊥AC，BE⊥AC，垂足分别为A、B．试说明AD+AB=BE．