如图甲所示,水平传送A、B两轮间的距离L="3.0" m,质量M="1.0" kg可视为质点的物块随传送带一起以恒定的速率v0向左匀速运动,当物块运动到最左端时,质量m=0.020kg的子弹以u0=400m/s的水平速度向右射中物块并穿出。在传送带的右端有一传感器,测出物块被击穿后的速度随时间的变化关系如图乙所示(图中取向右运动的方向为正方向,子弹射出物块的瞬间为t=0时刻)。子弹击穿物块的时间可忽略不计,且子弹不会击中传感器,物块的质量不因被子弹击穿而发生改变。不计空气阻力及A、B轮的大小,g=10m/s2。求:
(1)物块与传送带间的动摩擦因数m;
(2)第一颗子弹击穿物块后到物块与传送带相对静止期间,物块与传送带间相对运动的总路程;
(3)如果从第一颗子弹击中物块开始,每隔Dt="1.5" s就有一颗相同的子弹以同样的速度击穿物块,所有子弹与物块间的相互作用力均相同,直至物块最终离开传送带,整个过程中物块与传动带之间因摩擦而产生的热量Q。
民航客机机舱紧急出口的气囊是一条连接出口与地面的斜面,若斜面高为3米,斜面长为6米,质量60kg的人沿斜面下滑时所受的阻力是240N,求人滑到底端时的速度是多少?重力加速度g=10m/s2 。(提示:可用牛顿运动定律或动能定理,根据题意画出模型图或受力分析图得2--4分,写出公式或表达式得2--4分)
如图所示,在车厢中,一小球被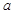 、
、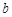 两根轻质细绳拴住,其中
两根轻质细绳拴住,其中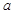 绳与竖直方向
绳与竖直方向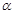 角,绳
角,绳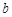 成水平状态,已知小球的质量为
成水平状态,已知小球的质量为 ,求:
,求: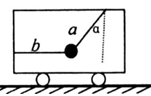
(1)车厢静止时,细绳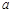 和
和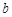 所受到的拉力;
所受到的拉力;
(2)当车厢以一定的加速度向右运动时,现要保持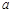 绳与竖直方向的夹角
绳与竖直方向的夹角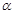 不变,求此时车厢的加速度大小。
不变,求此时车厢的加速度大小。
一般教室的门上都按装一种暗锁,这种暗锁由外壳A.骨架B.弹簧C(劲度系数为 )、锁舌D(倾斜角θ=45°,质量忽略不计)、锁槽E以及连杆、锁头等部件组成,如图甲所示(俯视图)。设锁舌D与外壳A和锁槽E之间的摩擦因数均为μ且最大静摩擦力与滑动摩擦力相等。有一次放学后,小明准备锁门,当他用某力拉门时,不能将门关上,此刻暗锁所处的状态如图乙所示,P为锁舌D与锁槽E之间的接触点,弹簧由于被压缩而缩短了
)、锁舌D(倾斜角θ=45°,质量忽略不计)、锁槽E以及连杆、锁头等部件组成,如图甲所示(俯视图)。设锁舌D与外壳A和锁槽E之间的摩擦因数均为μ且最大静摩擦力与滑动摩擦力相等。有一次放学后,小明准备锁门,当他用某力拉门时,不能将门关上,此刻暗锁所处的状态如图乙所示,P为锁舌D与锁槽E之间的接触点,弹簧由于被压缩而缩短了 ,问:
,问:
(1)此时,外壳A对所舌D的摩擦力的方向。
(2)此时,锁舌D与锁槽E之间的正压力的大小。
(3)当 满足一定条件时,无论用多大的力,也不能将门关上(这种现象称为自锁)。求暗锁能够保持自锁状态时μ的取值范围。
满足一定条件时,无论用多大的力,也不能将门关上(这种现象称为自锁)。求暗锁能够保持自锁状态时μ的取值范围。
超载和超速是造成交通事故的隐患之一。有一辆执勤的警车停在公路边,交警突然发现从他旁边 的速度匀速行驶的货车严重超载,他决定前去追赶,经过
的速度匀速行驶的货车严重超载,他决定前去追赶,经过 后发动警车,以
后发动警车,以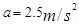 加速度做匀加速运动,但警车的最大速度是
加速度做匀加速运动,但警车的最大速度是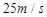 ,求:
,求:
(1)警车在追赶货车的过程中,两车间的最大距离是多少?
(2)警车发动后要多长时间才能追赶上货车?
有一种机械装置,叫做“滚珠式力放大器”,其原理如图所示,斜面A可以在光滑水平面上滚动,斜面B以及物体C都是被固定的,它们均由钢材制成,钢珠D置于A.B.C之间,当用水平力F推斜面A时,钢珠D受到物块C.斜面B的压力分别为 、
、 。已知斜面A.B的倾角分别为
。已知斜面A.B的倾角分别为 、
、 ,不计一切摩擦力及钢珠自身重力,试求
,不计一切摩擦力及钢珠自身重力,试求 、
、 的大小。
的大小。