一束平行光照射到半球形玻璃砖上,该束光线的边界分别为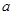 和
和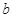 。已知玻璃砖半径为
。已知玻璃砖半径为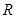 ,折射率为
,折射率为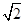 ,如下图所示,下边界
,如下图所示,下边界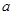 处光线恰好沿半径方向,在O点恰好产生全反射。求:
处光线恰好沿半径方向,在O点恰好产生全反射。求:
(1)玻璃砖发生全反射的临界角;
(2)光束ab在玻璃砖底产生的两个光斑的距离OB。
如图所示,质量为2m、高度为h的光滑弧形槽末端水平,放置在光滑水平地面上,质量为m的小球A从弧形槽顶端静止释放,之后与静止在水平面上质量为m的小球B发生对心碰撞并粘在一起.求: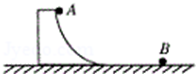
(1)小球A滑下后弧形槽的速度大小;
(2)小球A、B碰撞过程损失的机械能.
如图所示三个小球质量均为m,B、C两球用轻弹簧连接后放在光滑水平面上,A球以速度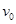 沿B、C两球的球心连线向B球运动,碰后A、B两球粘在一起。问:
沿B、C两球的球心连线向B球运动,碰后A、B两球粘在一起。问: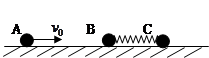
(1)A、B两球刚刚粘合在一起时的速度是多大?
(2)弹簧压缩至最短时三个小球的速度是多大?
(3)弹簧压缩至最短时弹簧的弹性势能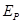 .
.
如图所示,在光滑水平面上有两个并排放置的木块A和B,已知mA=0.5kg,mB=0.3kg,有一质量为mC=0.1kg的小物块C以20m/s的水平速度滑上A表面,由于C和A、B间有摩擦,C滑到B表面上时最终与B共同以2.5m/s的速度运动,求: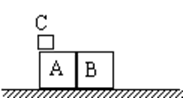
(1)木块A的最终速度;
(2)C滑离A木块的瞬时速度。
(注:衰变生成的新核均由X来表示)
(1)写出所给放射性元素的β衰变方程: (铋核)
(铋核)
(2)写出所给放射性元素的α衰变方程: (钍核)
(钍核)
(3)已知钍234的半衰期是24天,1g钍经过120天后还剩多少?
如图所示的竖直平面内,相距为d的不带电平行金属板M、N水平固定放置,与灯泡L、开关S组成回路并接地,上极板M与其上方空间的D点相距h,灯泡L的额定功率与电压分别为PL、UL。带电量为q的小物体以水平向右的速度v0从D点连续发射,落在M板其电荷立即被吸收,M板吸收一定电量后闭合开关S,灯泡能维持正常发光。设小物体视为质点,重力加速度为g,金属板面积足够大,M板吸收电量后在板面均匀分布,M、N板间形成匀强电场,忽略带电小物体间的相互作用。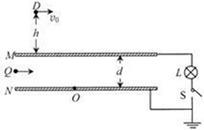
(1)初始时带电小物体落在M板上的水平射程为多少?
(2)单位时间发射小物体的个数为多少?
(3)闭合开关S后,带电粒子Q以水平速度从匀强电场左侧某点进入电场,并保持速度穿过M、N板之间。现若在M、N板间某区域加上方向垂直于纸面的匀强磁场,使Q在纸面内无论从电场左侧任何位置以某水平速度进入,都能到达N板上某定点O,求所加磁场区域为最小时的几何形状及位置。