(本小题满分12分)某中学准备在“植树节”来临之际,组织学生进行植树活动,学校学生会对一批花苗的高度(单位:cm),进行抽样检测,检测结果的频率分布直方图如图所示.根据标准, 花苗高度在区间[20,25)上的为一等品, 在区间[15,20)和区间[25,30)上的为二等品, 在区间[10,15)和[30,35)上的为三等品.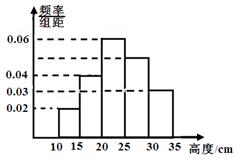
(Ⅰ)用频率估计概率, 现从该批花苗中随机抽取一株, 求其为二等品的概率;
(Ⅱ)已知检测结果为一等品的有6株,现随机从三等品中有放回地连续取两次,每次取1株,求取出的两株花苗中恰有1件的长度在区间[30,35)上的概率.
某项竞赛分别为初赛、复赛、决赛三个阶段进行,每个阶段选手要回答一个问题.规定
正确回答问题者进入下一阶段竞赛,否则即遭淘汰.已知某选手通过初赛、复赛、决赛的概率分别是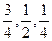 ,且各阶段通过与否相互独立.
,且各阶段通过与否相互独立.
(I)求该选手在复赛阶段被淘汰的概率;
(II)设该选手在竞赛中回答问题的个数为 ,求
,求 的分布列、数学期望和方差.
的分布列、数学期望和方差.
设集合 .
.
(Ⅰ)求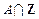 ;
;
(Ⅱ)若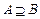 ,求
,求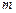 的取值范围.
的取值范围.
在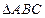 中,
中,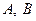 为锐角,角
为锐角,角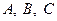 所对的边分别为
所对的边分别为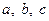 ,且
,且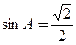 ,
,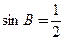 .
.
(Ⅰ)求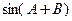 的值;
的值;
(Ⅱ)若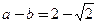 ,求
,求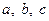 的值.
的值.
在平面直角坐标系中,O为坐标原点,已知两点M(1,—3)、N(5,1),若动点C满足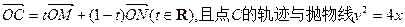 交于A、B两点。
交于A、B两点。
(I)求证: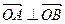 ;
;
(2)在x轴上是否存在一点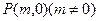 ,使得过点P的直线l交抛物线
,使得过点P的直线l交抛物线 于D、E两点,并以线段DE为直径的圆都过原点。若存在,请求出m的值,若不存在,请说明理由。
于D、E两点,并以线段DE为直径的圆都过原点。若存在,请求出m的值,若不存在,请说明理由。
如图,在四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点,PE⊥EC. 已知PD=
已知PD=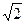 ,CD=2,AE=
,CD=2,AE= ,
,
(1)求证:平面PED⊥平面PEC
(2)求二面角E-PC-D的大小。