(本小题满分13分)已知抛物线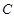 的顶点为坐标原点,焦点为
的顶点为坐标原点,焦点为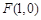 ,
,
(Ⅰ)求抛物线的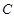 方程;
方程;
(Ⅱ)设是抛物线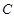 上的点,且满足
上的点,且满足 ,当
,当 的垂直平分线与
的垂直平分线与 轴交于点
轴交于点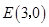 时,求
时,求 的面积.
的面积.
(本小题满分12分)
已知函数 ,在点
,在点 处的切线方程为
处的切线方程为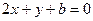 。
。
(1)求 与
与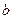 的值;
的值;
(2)求 的单调区间。
的单调区间。
(本小题满分12分)
设数列 的前n项和为
的前n项和为 ,且
,且 ,数列
,数列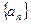 为等差数列,且
为等差数列,且
(1) 求数列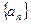 ,
, 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列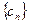 的前n项和
的前n项和 。
。
(本小题满分12分)
在 中,
中, ,记
,记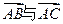 的夹角为
的夹角为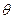 .
.
(Ⅰ)求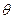 的取值范围;
的取值范围;
(Ⅱ)求函数 的最大值和最小值.
的最大值和最小值.
(本小题满分12分)
已知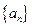 是首项为19,公差为-2的等差数列,
是首项为19,公差为-2的等差数列, 为
为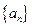 的前
的前 项和.
项和.
(1)当n为何值时 最大(用两种方法);
最大(用两种方法);
(2)设 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列 的通项公式及其前
的通项公式及其前 项和
项和 。
。
(本小题满分10分)
已知向量  =(cos
=(cos ,sin
,sin ),
), =(cos
=(cos ,sin
,sin ),|
),| |=
|= .
.
(Ⅰ)求cos( -
- )的值;
)的值;
(Ⅱ)若0< <
< ,-
,- <
< <0,且sin
<0,且sin =-
=- ,求sin
,求sin 的值.
的值.