(本小题满分13分)已知椭圆 过点
过点 ,且与抛物线
,且与抛物线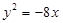 有一个公共的焦点.
有一个公共的焦点.
(Ⅰ)求椭圆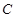 方程;
方程;
(Ⅱ)过椭圆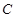 的右焦点
的右焦点 且斜率为
且斜率为 的直线
的直线 与椭圆
与椭圆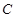 交于
交于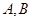 两点,求弦
两点,求弦 的长;
的长;
(Ⅲ)以第(Ⅱ)题中的 为边作一个等边三角形
为边作一个等边三角形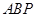 ,求点
,求点 的坐标.
的坐标.
(本小题满分12分)
甲、乙两位小学生各有2008年奥运吉祥物“福娃”5个(其中“贝贝”、“晶晶”、“欢欢”、
“迎迎”和“妮妮各一个”),现以投掷一个骰子的方式进行游戏,规则如下:当出现向上的点数是奇数时,甲赢得乙一个福娃;否则乙赢得甲一个福娃,规定掷骰子的次数达9次时,或在此前某人已赢得所有福娃时游戏终止.记游戏终止时投掷骰子的次数为
(1)求掷骰子的次数为7的概率;
(2)求 的分布列及数学期望E
的分布列及数学期望E .
.
(1)已知关于 的不等式
的不等式 在
在 上恒成立,求实数
上恒成立,求实数 的最小值;
的最小值;
(2)已知 ,求证:
,求证: .
.
(本小题满分10分)
已知曲线 的参数方程为
的参数方程为 (
( 为参数),曲线
为参数),曲线 的极坐标方程为
的极坐标方程为 .
.
(1)将曲线 的参数方程化为普通方程,将曲线
的参数方程化为普通方程,将曲线 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)曲线 ,
, 是否相交,若相交请求出公共弦的长,若不相交,请说明理由.
是否相交,若相交请求出公共弦的长,若不相交,请说明理由.
(本小题满分10分)
如图, 是⊙
是⊙ 的一条切线,切点为
的一条切线,切点为 ,
, 都是⊙
都是⊙ 的割线,已知
的割线,已知 .
.
(1)证明: ;
;
(2)证明: .
.
(本小题满分l2分)
已知函数 .
.
(1)求 的导数
的导数 ;
;
(2)求证:不等式 上恒成立;
上恒成立;
(3)求 的最大值.
的最大值.