在梯形ABCD中,AD∥BC,BA⊥AC,∠ABC = 450,AD = 2,BC = 6,以BC所在直线为x轴,建立如图所示的平面直角坐标系,点A在y轴上.
(1)求过A、D、C三点的抛物线的解析式;
(2)求△ADC的外接圆的圆心M的坐标,并求⊙M的半径;
(3)E为抛物线对称轴上一点,F为y轴上一点,求当ED+EC+FD+FC最小时,EF的长;
(4)设Q为射线CB上任意一点,点P为对称轴左侧抛物线上任意一点,问是否存在这样的点P、Q,使得以P、Q、C为顶点的三角形与△ADC相似?若存在,直接写出点P、Q的坐标,若不存在,则说明理由.
如图,已知点A(3,0),以A为圆心作⊙A与Y轴切于原点,与x轴的另一个交点为B,过B作⊙A的切线l.
(1)以直线l为对称轴的抛物线过点A及点C(0,9),求此抛物线的解析式;
(2)抛物线与x轴的另一个交点为D,过D作⊙A的切线DE,E为切点,求DE的长;
(3)点F是切线DE上的一个动点,当△BFD与△EAD相似时,求出BF的长 .
为了落实国家的惠农政策,某地政府制定了农户投资购买收割机的补贴办法,其中购买Ⅰ、Ⅱ两型收割机所投资的金额与政府补贴的额度存在下表所示的函数对应关系:
| Ⅰ型收割机 |
Ⅱ型收割机 |
||||
| 投资金额x(万元) |
x |
5 |
x |
2 |
4 |
| 补贴金额y(万元) |
y1=kx |
2 |
y2=ax2+bx |
2.4 |
3.2 |
(1)分别求出y1和y2的函数表达式;
(2)旺叔准备投资10万元购买Ⅰ、Ⅱ两型收割机。请你设计一个能获得最大补贴金额的方案,并求出按此方案能获得的补贴金额。
如图,已知二次函数y=ax2+bx+2的图像经过A(-1,-1),C(1,3).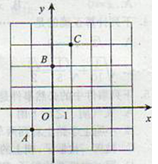
(1)求二次函数的解析式并画出它的图像;
(2)直接写出点A关于抛物线对称轴的对称点A'的坐标;
(3)求该抛物线上到x轴的距离为2的所有点的坐标。
如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C。
(1)求m的值;
(2)求点B的坐标;
(3)该二次函数图像上有一点D(x,y)(其中x>0,y>0),使S△ABD=S△ABC,求点D的坐标。
如图,以线段AB为直径的⊙O交线段AC于点E,点D是AE的中点,连接OD并延长交⊙O于点M,∠BOE=60°,cosC= ,BC=
,BC= .
.
(1)求 的度数;
的度数;
(2)求证:BC是⊙ 的切线;
的切线;
(3)求弧AM的长度.