在△ABC中，边BC的长与BC边上的高线长之和为20.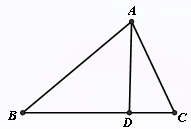
（1）写出△ABC的面积y与BC的长x之间的函数关系式。并写出自变量X的取值范围。
（2）当BC的长为多少时，△ABC的面积最大？最大面积是多少？
（贵港）已知：△ABC是等腰三角形，动点P在斜边AB所在的直线上，以PC为直角边作等腰三角形PCQ，其中∠PCQ=90°，探究并解决下列问题：
（1）如图①，若点P在线段AB上，且AC=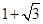
，PA=
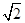，则：①线段PB= ，PC= ；
②猜想：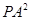
，
，
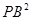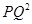三者之间的数量关系为 ；
（2）如图②，若点P在AB的延长线上，在（1）中所猜想的结论仍然成立，请你利用图②给出证明过程；
（3）若动点P满足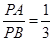
，求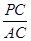
的值．（提示：请利用备用图进行探求）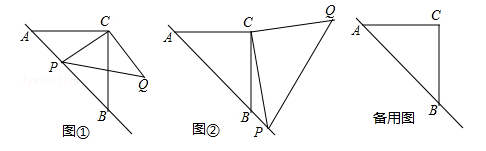
（贵港）（1）计算：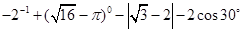
；
（2）解不等式组
，并在数轴上表示不等式组的解集．
（崇左）如图，点D在AB上，点E在AC上，AB=AC，AD=AE．求证：BE=CD．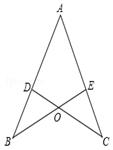
（崇左）计算：
．
（北海）如图1所示，已知抛物线
的顶点为D，与x轴交于A、B两点，与y轴交于C点，E为对称轴上的一点，连接CE，将线段CE绕点E按逆时针方向旋转90°后，点C的对应点C′恰好落在y轴上．
（1）直接写出D点和E点的坐标；
（2）点F为直线C′E与已知抛物线的一个交点，点H是抛物线上C与F之间的一个动点，若过点H作直线HG与y轴平行，且与直线C′E交于点G，设点H的横坐标为m（0＜m＜4），那么当m为何值时，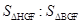
=5：6？
（3）图2所示的抛物线是由向右平移1个单位后得到的，点T（5，y）在抛物线上，点P是抛物线上O与T之间的任意一点，在线段OT上是否存在一点Q，使△PQT是等腰直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由．