（北海）如图1所示，已知抛物线
的顶点为D，与x轴交于A、B两点，与y轴交于C点，E为对称轴上的一点，连接CE，将线段CE绕点E按逆时针方向旋转90°后，点C的对应点C′恰好落在y轴上．
（1）直接写出D点和E点的坐标；
（2）点F为直线C′E与已知抛物线的一个交点，点H是抛物线上C与F之间的一个动点，若过点H作直线HG与y轴平行，且与直线C′E交于点G，设点H的横坐标为m（0＜m＜4），那么当m为何值时，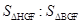
=5：6？
（3）图2所示的抛物线是由向右平移1个单位后得到的，点T（5，y）在抛物线上，点P是抛物线上O与T之间的任意一点，在线段OT上是否存在一点Q，使△PQT是等腰直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由．
如图，要设计一个矩形的花坛，花坛长60 m，宽40 m，有两条纵向甬道和一条横向甬道，横向甬道的两侧有两个半圆环形甬道，半圆环形甬道的内半圆的半径为10 m，横向甬道的宽度是其它各甬道宽度的2倍．设横向甬道的宽为2x m．（π的值取3）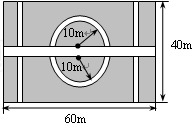
（1）用含x的式子表示两个半圆环形甬道的面积之和；
（2）当所有甬道的面积之和比矩形面积的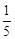
多36 m2时，求x的值．
有四张背面相同的纸牌
，其正面分别画有四个不同的几何图形（如图）．小明将这4张纸牌背面朝上洗匀后摸出一张，将剩余3张洗匀后再摸出一张．
（1）用树状图（或列表法）表示两次摸牌所有可能出现的结果（纸牌用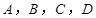
表示）；
（2）求摸出的两张牌面图形既是轴对称图形又是中心对称图形纸牌的概率．
已知：如图，E、F是平行四边形ABCD的对角线AC上的两点，AE=CF.
求证：（1）△ADF≌△CBE；（2）EB∥DF.
解方程：（1）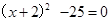 
；（2）x2+4x－2=0（用配方法）；（3）
．
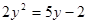课本中把长与宽之比为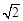
的矩形纸片称为标准纸．请解决下列问题：
（1）将一张标准纸ABCD(AB＜BC)对开，如图1所示，所得的矩形纸片ABEF是标准纸．请给予证明；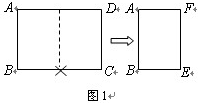
（2）在一次综合实践课上，小明尝试着将矩形纸片ABCD(AB＜BC)进行如下操作：
第一步：沿过A点的直线折叠，使B点落在AD边上点F处，折痕为AE(如图2甲)；
第二步：沿过D点的直线折叠，使C点落在AD边上点N处，折痕为DG(如图2乙) ．此时E点恰好落在AE边上的点M处；
第三步：沿直线DM折叠（如图2丙），此时点G恰好与N点重合．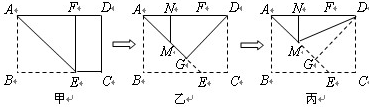
请你研究，矩形纸片ABCD是否是一张标准纸？请说明理由．
（3）不难发现，将一张标准纸如图3一次又一次对开后，所得的矩形纸片都是标准纸．现有一张标准纸ABCD，AB＝1，BC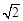＝，问第5次对开后所得标准纸的周长是多少？探索并直接写出第2002次对开后所得标准纸的周长．