有四张背面相同的纸牌 ,其正面分别画有四个不同的几何图形(如图).小明将这4张纸牌背面朝上洗匀后摸出一张,将剩余3张洗匀后再摸出一张.
,其正面分别画有四个不同的几何图形(如图).小明将这4张纸牌背面朝上洗匀后摸出一张,将剩余3张洗匀后再摸出一张.
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌用 表示);
表示);
(2)求摸出的两张牌面图形既是轴对称图形又是中心对称图形纸牌的概率.
某村2016年的人均收入为20000元,2018年的人均收入为24200元
(1)求2016年到2018年该村人均收入的年平均增长率;
(2)假设2019年该村人均收入的增长率与前两年的年平均增长率相同,请你预测2019年该村的人均收入是多少元?
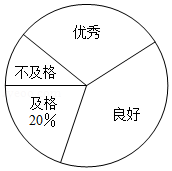
某校为了解八年级男生“立定跳远”成绩的情况,随机选取该年级部分男生进行测试,以下是根据测试成绩绘制的统计图表的一部分.
|
成绩等级 |
频数(人 |
频率 |
|
优秀 |
15 |
0.3 |
|
良好 |
||
|
及 格 |
||
|
不及格 |
5 |
根据以上信息,解答下列问题
(1)被测试男生中,成绩等级为“优秀”的男生人数为 人,成绩等级为“及格”的男生人数占被测试男生总人数的百分比为 ;
(2)被测试男生的总人数为 人,成绩等级为“不及格”的男生人数占被测试男生总人数的百分比为 ;
(3)若该校八年级共有180名男生,根据调查结果,估计该校八年级男生成绩等级为“良好”的学生人数.
如图,点 , 在 上, , , ,求证: .

如图,在平面直角坐标系中,直线 与 轴交于点 ,与 轴交点 ,抛物线 过 , 两点,与 轴交于另一点 .
(1)求抛物线的解析式.
(2)在直线 上方的抛物线上有一动点 ,连接 ,与直线 相交于点 ,当 时,求 的值.
(3)点 是抛物线对称轴上一点,在(2)的条件下,若点 位于对称轴左侧,在抛物线上是否存在一点 ,使以 , , , 为顶点的四边形是平行四边形?若存在,直接写出点 的坐标;若不存在,请说明理由.

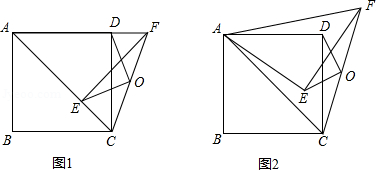
如图,四边形 是正方形,连接 ,将 绕点 逆时针旋转 得 ,连接 , 为 的中点,连接 , .
(1)如图1,当 时,请直接写出 与 的关系(不用证明).
(2)如图2,当 时,(1)中的结论是否成立?请说明理由.
(3)当 时,若 ,请直接写出点 经过的路径长.