已知函数 .
.
(1)证明: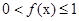 ;
;
(2)当 时,
时, ,求
,求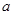 的取值范围.
的取值范围.
已知抛物线 ,直线
,直线 与E交于A、B两点,且
与E交于A、B两点,且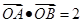 ,其中O为原点.
,其中O为原点.
(1)求抛物线E的方程;
(2)点C坐标为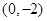 ,记直线CA、CB的斜率分别为
,记直线CA、CB的斜率分别为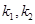 ,证明:
,证明: 为定值.
为定值.
据民生所望,相关部门对所属单位进行整治性核查,标准如下表: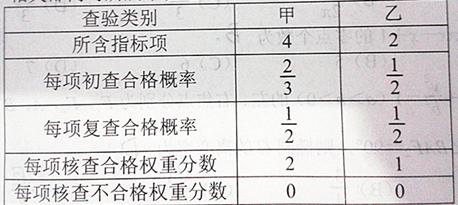
规定初查累计权重分数为10分或9分的不需要复查并给予奖励,10分的奖励18万元;9分的奖励8万元;初查累计权重分数为7分及其以下的停下运营并罚款1万元;初查累计权重分数为8分的要对不合格指标进行复查,最终累计权重得分等于初查合格部分与复查部分得分的和,最终累计权重分数为10分方可继续运营,否则停业运营并罚款1万元.
(1)求一家单位既没获奖励又没被罚款的概率;
(2)求一家单位在这次整治性核查中所获金额X(万元)的分布列和数学期望(奖励为正数,罚款为负数).
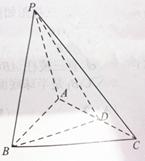
如图,在三棱锥 中,
中, ,
,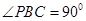 ,D为AC的中点,
,D为AC的中点,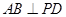 .
.
(1)求证:平面 平面
平面 ;
;
(2)求二面角 的余弦值.
的余弦值.
在锐角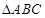 中,
中, 分别为角
分别为角 的对边,且
的对边,且 .
.
(1)求角A的大小;
(2)若BC边上高为1,求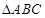 面积的最小值?
面积的最小值?