集合A是由具备下列性质的函数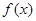 组成的:
组成的:
(1)函数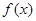 的定义域是
的定义域是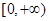 ; (2)函数
; (2)函数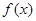 的值域是
的值域是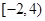 ;
;
(3)函数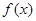 在
在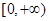 上是增函数.试分别探究下列两小题:
上是增函数.试分别探究下列两小题:
(1)判断函数 ,及
,及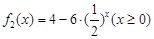 是否属于集合A?并证明.
是否属于集合A?并证明.
(2)对于(1)中你认为属于集合A的函数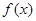 ,不等式
,不等式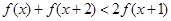 是否对于任意的
是否对于任意的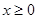 总成立?若不成立,为什么?若成立,请证明你的结论.
总成立?若不成立,为什么?若成立,请证明你的结论.
【改编】(本小题满分14分)已知函数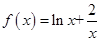 .
.
(1)求函数的单调增区间;
(2)若 ,求实数
,求实数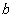 的取值范围.
的取值范围.
如图,在四棱锥P-ABCD中,ABCD为平行四边形, 平面PAB,
平面PAB,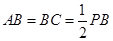 ,
,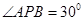 .M为PB的中点.
.M为PB的中点.
(1)求证:PD//平面AMC;
(2)求锐二面角B-AC-M的余弦值.
(本小题满分12分)小王在某社交网络的朋友圈中,向在线的甲、乙、丙随机发放红包,每次发放1个.
(Ⅰ)若小王发放5元的红包2个,求甲恰得1个的概率;
(Ⅱ)若小王发放3个红包,其中5元的2个,10元的1个.记乙所得红包的总钱数为X,求X的分布列和期望.
【改编】【2014年广东省东莞市高三第二次模拟理】已知函数 .
.
(1)求函数 的图象的对称中心;
的图象的对称中心;
(2)在△ABC中,三内角A,B,C的对边分别为a,b,c,已知 ,b,a,c成等差数列,且
,b,a,c成等差数列,且 ,求a的值.
,求a的值.
(本小题满分14分)已知函数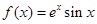
(1)求函数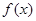 的单调区间;
的单调区间;
(2)当 时,
时,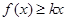 ,求实数
,求实数 的取值范围
的取值范围