(本小题满分12分)某校在一次对学生在课外活动中喜欢跑步和喜欢打球的学生的抽样调查中,随机抽取了100名同学,相关数据如下表所示:
| |
喜欢跑步 |
喜欢打球 |
总计 |
| 男生 |
23 |
32 |
55 |
| 女生 |
29 |
16 |
45 |
| 总计 |
52 |
48 |
100 |
(1)由表中数据直观分析,喜欢打球的学生是否与性别有关?
(2)用分层抽样的方法在喜欢打球的学生中随机抽取6名,男学生应该抽取几名?
(3)在上述抽取的6名学生中任取2名,求恰有1名女学生的概率.
已知椭圆 的焦点为
的焦点为 ,抛物线
,抛物线 与椭圆在第一象限的交点为
与椭圆在第一象限的交点为 ,若
,若 。
。
(1)求 的面积;
的面积;
(2)求此抛物线的方程。
在平面直角坐标系 中,点P到两点
中,点P到两点 ,
,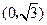 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为 .
.
(1)写出 的方程;
的方程;
(2)设直线 与
与 交于
交于 两点,
两点, 为何值时
为何值时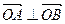 ?
?
已知圆心为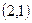 的圆
的圆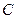 与直线
与直线 相切。
相切。
(1)求圆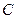 的标准方程;
的标准方程;
(2)若圆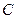 与圆
与圆 相交于
相交于 两点,求直线
两点,求直线 的方程。(用一般式表示)
的方程。(用一般式表示)
已知动圆C过点A(-2,0),且与圆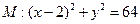 相内切。
相内切。
(1)求动圆C的圆心的轨迹方程;
(2)设直线 : y=kx+m(其中k,m∈Z)与(1)所求轨迹交于不同两点B,D,与双曲线
: y=kx+m(其中k,m∈Z)与(1)所求轨迹交于不同两点B,D,与双曲线 交于不同两点E,F,问是否存在直线
交于不同两点E,F,问是否存在直线 ,使得向量
,使得向量 ,若存在,指出这样的直线有多少条?若不存在,请说明理由
,若存在,指出这样的直线有多少条?若不存在,请说明理由
已知椭圆 ,直线
,直线 与椭圆交于A、B两点,M是线段AB的中点,连接OM并延长交椭圆于点C.直线AB与直线OM的斜率分别为k、m,且
与椭圆交于A、B两点,M是线段AB的中点,连接OM并延长交椭圆于点C.直线AB与直线OM的斜率分别为k、m,且 .
.
(1)求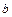 的值;
的值;
(2)若直线AB经过椭圆的右焦点F,问:对于任意给定的不等于零的实数k,是否存在a∈ ,使得四边形OACB是平行四边形,请证明你的结论;
,使得四边形OACB是平行四边形,请证明你的结论;