已知函数y=f(x)满足:对任意的x1<x2≤-1,[f(x2)-f(x1)](x2-x1)>0恒成立,则f(-2),f(-
),f(-1)的大小关系为( )
| A．f(-2)<f(-)<f(-1) |
| B．f(-2)>f(-)>f(-1) |
| C．f(-2)>f(-1)>f(-) |
| D．f(-)>f(-2)>f(-1) |
已知函数f(x)=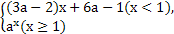
单调递减,那么实数a的取值范围是( )
| A．(0,1) | B．(0, ) |
C．[ ,) |
D．[,1) |
已知函数f(x)=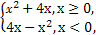
若f(2-a2)>f(a),则实数a的取值范围是( )
| A．(-∞,-1)∪(2,+∞) |
| B．(-1,2) |
| C．(-2,1) |
| D．(-∞,-2)∪(1,+∞) |
若函数y=ax与y=-
在(0,+∞)上都是减函数,则y=ax2+bx在(0,+∞)上是( )
| A．增函数 | B．减函数 | C．先增后减 | D．先减后增 |
函数f(x)=1-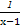
( )
| A．在(-1,+∞)上单调递增 |
| B．在(1,+∞)上单调递增 |
| C．在(-1,+∞)上单调递减 |
| D．在(1,+∞)上单调递减 |
，则“
”是“
”的