(本小题满分12分) 已知中心在原点,焦点在 轴上的椭圆C的离心率为
轴上的椭圆C的离心率为 ,且经过点
,且经过点 .
.
(1)求椭圆C的方程;
(2)是否存在过点 的直线
的直线 与椭圆C相交于不同的两点
与椭圆C相交于不同的两点 ,满足
,满足 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
已知等差数列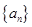 的首项
的首项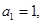 公差
公差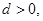 且
且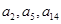 分别是等比数列
分别是等比数列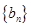 的
的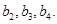
(1)求数列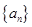 和
和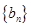 的通项公式;
的通项公式;
(2)设数列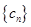 对任意正整数
对任意正整数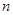 均有
均有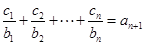 成立,求
成立,求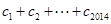 的值.
的值.
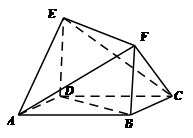
如图所示的多面体中,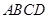 是菱形,
是菱形,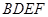 是矩形,
是矩形,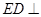 面
面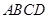 ,
,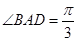 .
.
(1)求证: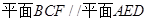 .
.
(2)若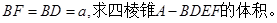
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| 喜爱打篮球 |
不喜爱打篮球 |
合计 |
|
| 男生 |
20 |
5 |
25 |
| 女生 |
10 |
15 |
25 |
| 合计 |
30 |
20 |
50 |
(1)用分层抽样的方法在喜欢打蓝球的学生中抽6人,其中男生抽多少人?
(2)在上述抽取的6人中选2人,求恰有一名女生的概率.
设函数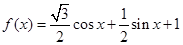
(1)求函数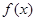 的值域和函数的单调递增区间;
的值域和函数的单调递增区间;
(2)当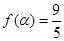 ,且
,且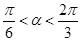 时,求
时,求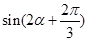 的值.
的值.
已知关于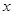 的函数
的函数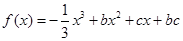 ,其导函数为
,其导函数为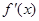 .记函数
.记函数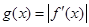 在区间
在区间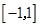 上的最大值为
上的最大值为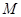 .
.
(1) 如果函数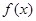 在
在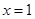 处有极值
处有极值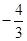 ,试确定
,试确定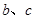 的值;
的值;
(2) 若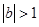 ,证明对任意的
,证明对任意的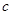 ,都有
,都有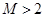 ;
;
(3) 若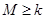 对任意的
对任意的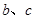 恒成立,试求
恒成立,试求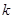 的最大值.
的最大值.