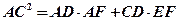已知函数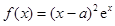 在
在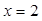 时取得极小值.
时取得极小值.
(1)求实数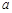 的值;
的值;
(2)是否存在区间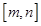 ,使得
,使得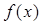 在该区间上的值域为
在该区间上的值域为 ?若存在,求出
?若存在,求出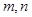 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(本小题满分10分)
已知在(1-2log2x)n的展开式中所有奇数项的二项式系数的和为64.
(1)求n的值;
(2)求展开式中所有项的系数之和.
如图,
的角平分线
的延长线交它的外接圆于点
. 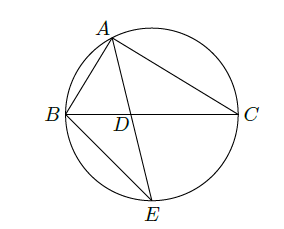
(Ⅰ)证明:
;
(Ⅱ)若
的面积
,求
的大小.
(本小题满分10分)选修4-5:不等式选讲
已知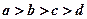 ,求证:
,求证: .
.
(本小题满分10分)选修4-4:坐标系与参数方程
已知圆锥曲线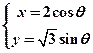 (
( 是参数)和定点
是参数)和定点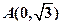 ,
, 是圆锥曲线的左、右焦点。
是圆锥曲线的左、右焦点。
(1)求经过点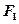 垂直于直线
垂直于直线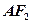 的直
的直 线l的参数方程;
线l的参数方程;
(2)以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,求直线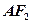 的极坐标方程.
的极坐标方程.
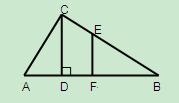
(本小题满分10分)选修4-1:几何证明选讲如图,CD是Rt△ABC的斜边AB上的高, E是BC上任意一点,EF⊥AB于F。
E是BC上任意一点,EF⊥AB于F。
求证: