如图,在三棱锥S—ABC中,SA丄平面ABC,SA = 3,AC=2,AB丄BC,点P是SC的中点,则异面直线SA与PB所成角的正弦值为
A. |
B. |
C. |
D. |
设复数z=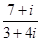 -isinθ,其中i为虚数单位,θ∈[-
-isinθ,其中i为虚数单位,θ∈[-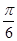 ,
, ],则|z|的取值范围是( )
],则|z|的取值范围是( )
A.[1, ] ] |
B.[1,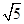 ] ] |
C.[ , ,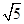 ] ] |
D.[ , ,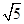 ] ] |
设复数z=-1-i(i为虚数单位),z的共轭复数为 ,则|(1-z)·
,则|(1-z)· |=( )
|=( )
A. |
B.2 | C. |
D.1 |
已知复数z1=1+i,z2=1+bi,i为虚数单位,若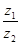 为纯虚数,则实数b的值是( )
为纯虚数,则实数b的值是( )
| A.1 | B.-1 | C.2 | D.-2 |
已知复数z满足(1+i)z=3+i(i为虚数单位),则复数z在复平面内对应的点位于( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
下面命题:
①0比-i大;
②两个复数互为共轭复数,当且仅当和为实数时成立;
③x+yi=1+i的充要条件为x=y=1;
④如果让实数a与ai对应,那么实数集与纯虚数集一一对应.
其中正确命题的个数是( )
| A.0 | B.1 | C.2 | D.3 |