【问题情境】
徐老师给爱好学习的小敏和小捷提出这样一个问题:
如图1,△ABC中,∠B=2∠C,AD是∠BAC的平分线.求证:AB+BD=AC
小敏的证明思路是:在AC上截取AE=AB,
连接DE.(如图2)
小捷的证明思路是:延长CB至点E,使BE=AB,连接AE.可以证得:AE=DE(如图3)
请你任意选择一种思路继续完成下一步的证明.
【变式探究】
“AD是∠BAC的平分线”改成“AD是BC边上的高”,其它条件不变.(如图4)
AB+BD=AC成立吗?若成立,请证明;若不成立,写出你的正确结论,并说明理由.
【迁移拓展】
△ABC中,∠B=2∠C.求证: .(如图5)
.(如图5)
解方程: .
.
解方程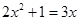
(本题满分12分) 如图,在平面直角坐标系中,抛物线与x轴交于点A、B
(点A在点B的左侧),与y轴交于点C(0,4),顶点为(1,).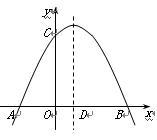
(1)求抛物线的函数解析式;
(2)抛物线的对称轴与x轴交于点D,点P在对称轴上且使△CDP为等腰三角形.请直接写出满足条件的所有点的坐标P;
(3)若点E是线段AB上的一个动点(与点A、B不重合),连接AC、BC,过点E作EF∥AC交线段BC于点F,连接CE,记△CEF的面积为S,S是否存在最大值?若存在,请求出S的最大值及此时点E的坐标;若不存在,请说明理由.
(本题满分12分) 某工厂有一种材科,可加工甲、乙、丙三种型号机械配件共240个.厂方计划由20个工人一天内加工完成.并要求每人只加工一种配件.根据下表提供的信息。解答下列问题:
(1)设加工甲种配件的人数为x,加工乙种配件的人数为y,求y与x之间的函数关系式。
(2)如果加工每种配件的人数均不少于3人.那么加工配件的人数安排方案有几种?写出每种安排方案.
(3)要使此次加工配件的利润最大,应采用(2)中哪种方案?并求出最大利润值.
(本题满分10分) 面对全球金融危机的挑战,我国政府毅然启动内需,改善民生.国务院决定从2009年2月1日起,“家电下乡”在全国范围内实施,农民购买人选产品,政府按原价购买总额的13%给予补贴返还.某村委会组织部分农民到商场购买人选的同一型号的冰箱、电视机两种家电,已知购买冰箱的数量是电视机的2倍,且按原价购买冰箱总额为40000元、电视机总额为15000元.根据“家电下乡”优惠政策,每台冰箱补贴返还的金额比每台电视机补贴返还的金额多65元,求冰箱、电视机各购买多少台?
(1)设购买电视机 台,依题意填充下列表格:
台,依题意填充下列表格:
 项目 项目家电种类 |
购买数量(台) |
原价购买总额(元) |
政府补贴返还比例 |
补贴返还总金额(元) |
每台补贴返还金额(元) |
| 冰箱 |
40 000 |
13% |
|||
| 电视机 |
 |
15 000 |
13% |
(2)列出方程(组)并解答.