(本小题满分12分)椭圆C: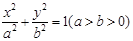 的长轴是短轴的两倍,点
的长轴是短轴的两倍,点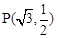 在椭圆上.不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为
在椭圆上.不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为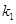 、
、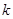 、
、 ,且
,且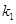 、
、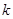 、
、 恰好构成等比数列,记△
恰好构成等比数列,记△ 的面积为S.
的面积为S.
(Ⅰ)求椭圆C的方程.
(Ⅱ)试判断 是否为定值?若是,求出这个值;若不是,请说明理由?
是否为定值?若是,求出这个值;若不是,请说明理由?
(Ⅲ)求S的范围.
设△ABC的三个内角A,B,C所对的边长分别为a,b,c.平面向量 = (cosA,cosC),
= (cosA,cosC),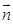 =(c,a),
=(c,a),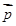 =(2b,0),且
=(2b,0),且 ·(
·(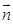 -
-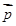 )=0
)=0
(1)求角A的大小;
(2)当|x|≤A时,求函数f(x)=sinxcosx+sinxsin(x- )的值域.
)的值域.
设命题p:|2x-3|<1;命题q:lg2x-(2t+l)lgx+t(t+l)≤0,
(1)若命题q所表示不等式的解集为A={x|l0≤x≤100},求实数t的值;
(2)若 p是
p是 q的必要不充分条件,求实数t的取值范围.
q的必要不充分条件,求实数t的取值范围.
已知函数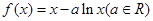 .
.
(Ⅰ)当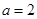 时,求曲线
时,求曲线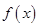 在
在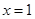 处的切线方程;
处的切线方程;
(Ⅱ)设函数 ,求函数
,求函数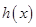 的单调区间;
的单调区间;
(Ⅲ)若 ,在
,在 上存在一点
上存在一点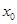 ,使得
,使得 成立,求
成立,求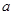 的取值范围.
的取值范围.
四棱锥A-BCDE的正视图和俯视图如下,其中正视图是等边三角形,俯视图是直角梯形.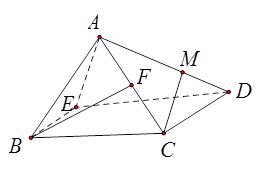
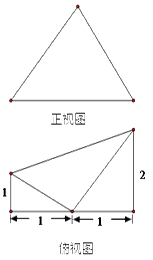
(Ⅰ)若F为AC的中点,当点M在棱AD上移动,是否总有BF丄CM,请说明理由.
(Ⅱ)求三棱锥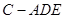 的高.
的高.
已知等比数列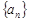 是递增数列,
是递增数列,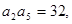
 ,数列
,数列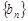 满足
满足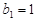 ,且
,且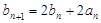 (
(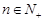 )
)
(Ⅰ)证明:数列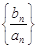 是等差数列;
是等差数列;
(Ⅱ)若对任意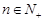 ,不等式
,不等式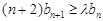 总成立,求实数
总成立,求实数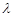 的最大值.
的最大值.