(本小题满分10分)选修4—1:几何证明选讲
如图,四边形ACED是圆内接四边形,延长AD与CE的延长线交于点B,且AD=DE,AB=2AC.
(Ⅰ)求证:BE=2AD;
(Ⅱ)当AC=2,BC=4时,求AD的长.

(1)若 ,求
,求 ;
;
(2)若函数 对应的图象记为
对应的图象记为
(3)求曲线 在
在 处的切线方程?(II)若直线
处的切线方程?(II)若直线 为曲线
为曲线 的切线,并且直线
的切线,并且直线 与曲线
与曲线 有且仅有一个公共点,求所有这样直线
有且仅有一个公共点,求所有这样直线 的方程?
的方程?
已知在递增等差数列 中,
中, ,
, 成等比数列数列
成等比数列数列 的前n项和为Sn,且
的前n项和为Sn,且 .
.
(1)求数列 、
、 的通项公式;(2)设
的通项公式;(2)设 ,求数列
,求数列 的前
的前 和
和 .
.
在 中,角
中,角 ,
, ,
, 的对边分别为
的对边分别为 ,且
,且 ,
, ,
, 成等差数列.
成等差数列.
(1)若 ,求
,求 的值;(2)求sinA+sinC的最大值.
的值;(2)求sinA+sinC的最大值.
已知函数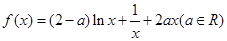
(1)当 时,求
时,求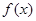 的极值
的极值
(2)当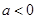 时,求
时,求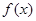 的单调区间
的单调区间
(3)若对任意的 ,恒有
,恒有 成立,求实数
成立,求实数 的取值范围。
的取值范围。
已知向量a=(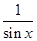 ,
, ),b=(2,cos2x).
),b=(2,cos2x).
(1)若x∈(0, ],试判断a与b能否平行?
],试判断a与b能否平行?
(2)若x∈(0, ],求函数f(x)=a·b的最小值.
],求函数f(x)=a·b的最小值.