(本小题共14分)如图,将矩形ABCD沿对角线BD把△ABD折起,使A点移到 点,且
点,且 在平面BCD上的射影O恰好在CD上.
在平面BCD上的射影O恰好在CD上.
(1)求证:BC⊥ ;
;
(2)求证:平面 ⊥平面
⊥平面 ;
;
(3)若AB=10,BC=6,求三棱锥 的体积.
的体积.
经过长期观察得到:在交通繁忙的时段内,某公路汽车的车流量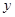 (千辆/小时)与汽车的平均速度
(千辆/小时)与汽车的平均速度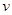 (千米/小时)之间的函数关系为
(千米/小时)之间的函数关系为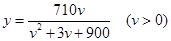
(1)在该时段内,当汽车的平均速度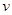 为多少时,车流量最大,最大车流量为多少?(精确到0.1千辆/小时)
为多少时,车流量最大,最大车流量为多少?(精确到0.1千辆/小时)
(2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?
等差数列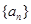 中,
中,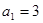 ,其前
,其前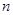 项和为
项和为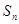 .等比数列
.等比数列 的各项均为正数,
的各项均为正数,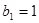 ,且
,且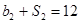 ,
,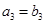 .
.
(Ⅰ)求数列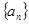 与
与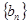 的通项公式;
的通项公式;
(Ⅱ)求数列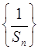 的前
的前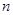 项和
项和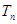 .
.
已知p: 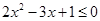 ,q:
,q: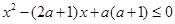
(1)若a=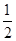 ,且
,且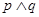 为真,求实数x的取值范围;
为真,求实数x的取值范围;
(2)若p是q的充分不必要条件,求实数a的取值范围.
在 中,
中, 分别为角
分别为角 所对的边,角
所对的边,角 是锐角,且
是锐角,且 .
.
(Ⅰ)求角 的值;
的值;
(Ⅱ)若 ,
, 的面积为
的面积为 ,求
,求 的值.
的值.
如图,在等腰直角三角形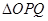 中,
中, ,
,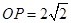 ,点
,点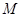 在线段
在线段 上.
上.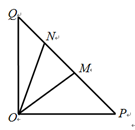
(1)若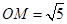 ,求
,求 的长;
的长;
(2)若点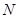 在线段
在线段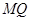 上,且
上,且 ,问:当
,问:当 取何值时,
取何值时,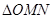 的面积最小?并求出面积的最小值.
的面积最小?并求出面积的最小值.