(本小题满分12分)如图1,平面四边形ABCD关于直线AC对称,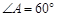 ,
, ,
, ,把△ABD沿BD折起(如图2),使二面角
,把△ABD沿BD折起(如图2),使二面角 为直二面角.如图2,
为直二面角.如图2,
(Ⅰ)求AD与平面ABC所成的角的余弦值;
(Ⅱ)求二面角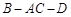 的大小的正弦值.
的大小的正弦值.
(本小题满分12分)
已知两直线 :
: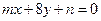 和
和 :
: ,
,
(1)若 与
与 交于点
交于点 ,求
,求 的值;
的值;
(2)若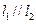 ,试确定
,试确定 需要满足的条件;
需要满足的条件;
(3)若l1⊥l2 ,试确定 需要满足的条件.
需要满足的条件.
(本小题满分10分)
如图所示的一个三视图中,右面是一个长方体截去一角所得多面体的直观图,它的正视 图和侧视图在下面画出(单位:cm)
图和侧视图在下面画出(单位:cm)

(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图;
(2)按照给出的尺寸,求该多面体的体积;
(本小题满分10分)
甲、乙、丙三名射击运动员射中目标的概率分别为
 ,三人各射击一次,击中目标的次数记为
,三人各射击一次,击中目标的次数记为 .
.
(1)求 的分布列及
的分布列及 数学期望;
数学期望;
(2)在概率 (
( =0,1,2,3)中, 若
=0,1,2,3)中, 若 的值最大, 求实数
的值最大, 求实数 的取值范围.
的取值范围.
(本小题满分10分)
已知动圆 过点
过点 且与直线
且与直线 相切.
相切.
(1)求点 的轨迹
的轨迹 的方程;
的方程;
(2)过点 作一条直线交轨迹
作一条直线交轨迹 于
于 两点,轨迹
两点,轨迹 在
在 两点处的切线相交于点
两点处的切线相交于点 ,
, 为线段
为线段 的中点,求证:
的中点,求证: 轴.
轴.
D.选修4—5:不等式选讲
(本小题满分10分)
求函数 的最大值.
的最大值.