在四边形 中,有下列条件:① ;② ;③ ;④ .
(1)从中任选一个作为已知条件,能判定四边形 是平行四边形的概率是 .
(2)从中任选两个作为已知条件,请用画树状图或列表的方法表示能判定四边形 是矩形的概率,并判断能判定四边形 是矩形和是菱形的概率是否相等?
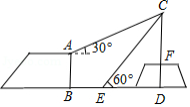
如图, 是某景区内高 的观景台, 是与 底部相平的一座雕像(含底座),在观景台顶 处测得雕像顶 点的仰角为 ,从观景台底部 处向雕像方向水平前进 到达点 ,在 处测得雕像顶 点的仰角为 ,已知雕像底座 高 ,求雕像 的高.(结果保留根号)
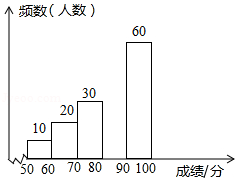
为打造平安校园,增强学生安全防范意识,某校组织了全校1200名学生参加校园安全网络知识竞赛.赛后随机抽取了其中200名学生的成绩作为样本进行整理,并制作了如下不完整的频数分布表和频数分布直方图.
|
成绩 分 |
频数 |
频率 |
|
|
10 |
|
|
|
20 |
0.10 |
|
|
30 |
0.15 |
|
|
|
0.40 |
|
|
60 |
0.30 |
请根据图表提供的信息,解答下列各题:
(1)表中 , ,请补全频数分布直方图.
(2)若用扇形统计图来描述成绩分布情况,则分数段 对应扇形的圆心角的度数是 .
(3)若成绩在80分以上(包括80分)为合格,则参加这次竞赛的1200名学生中成绩合格的大约有多少名?
如图,在平面直角坐标系中,抛物线 与 轴交于 , 两点,点 ,经过点 的直线 与抛物线的另一交点为 ,与 轴交点为 ,点 是直线 下方的抛物线上的一个动点(不与点 , 重合).
(1)求该抛物线的解析式.
(2)过点 作 ,垂足为点 ,作 轴交直线 于点 ,设点 的横坐标为 ,线段 的长度为 ,求 与 的函数关系式.
(3)点 在抛物线的对称轴上运动,当 是以 为直角边的等腰直角三角形时,请直接写出符合条件的点 的坐标.

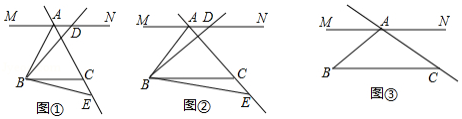
中, , ,过点 作直线 ,使 ,点 在直线 上,作射线 ,将射线 绕点 顺时针旋转角 后交直线 于点 .
(1)如图①,当 ,且点 在射线 上时,直接写出线段 , , 的数量关系.
(2)如图②,当 ,且点 在射线 上时,直写出线段 、 、 的数量关系,并说明理由.
(3)当 时,若点 在射线 上, , ,请直接写出线段 的长度.