如图:抛物线y=-x2+bx+c交x轴于A、B,直线y=x+2过点A,交y轴于C,交抛物线于D,且D的纵坐标为5.
(1)求抛物线解析式;
(2)点P为抛物线在第一象限的图象上一点,直线PC交x轴于点E,若PC=3CE,求点P的坐标;
(3)在(2)的条件下,点Q为x轴上一点,把△PCQ沿CQ翻折,点P刚好落在x轴上点G处,求Q点的坐标.
如图,一只猫头鹰蹲在一棵树AC的B(点B在AC上)处,发现一只老鼠躲进短墙DF的另一侧,猫头鹰的视线被短墙遮住,为了寻找这只老鼠,它又飞至树顶C处,已知短墙高DF=4米,短墙底部D与树的底部A的距离为2.7米,猫头鹰从C点观测F点的俯角为53°,老鼠躲藏处M(点M在DE上)距D点3米.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)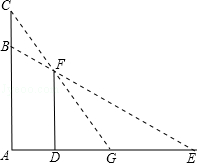
(1)猫头鹰飞至C处后,能否看到这只老鼠?为什么?
(2)要捕捉到这只老鼠,猫头鹰至少要飞多少米(精确到0.1米)?
夏季来临,天气逐渐炎热起来,某商店将某种碳酸饮料每瓶的价格上调了10%,将某种果汁饮料每瓶的价格下调了5%,已知调价前买这两种饮料个一瓶共花费7元,调价后买上述碳酸饮料3瓶和果汁饮料2瓶共花费17.5元,问这两种饮料在调价前每瓶各多少元?
小亮和小莹自制了一个标靶进行投标比赛,两人各投了10次,如图是他们投标成绩的统计图.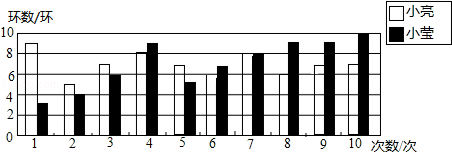
(1)根据图中信息填写下表
| 平均数 |
中位数 |
众数 |
|
| 小亮 |
7 |
||
| 小莹 |
7 |
9 |
(2)分别用平均数和中位数解释谁的成绩比较好.
如图,四边形ABCD中,∠A=∠BCD=90°,BC=CD,CE⊥AD,垂足为E,求证:AE=CE.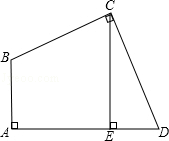
计算: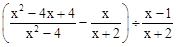 -.
-.