如图，在平面直角坐标系中，抛物线y=ax2+bx+6经过点A（-3，0）和点B（2，0）．直线y=h（h为常数，且0＜h＜6）与BC交于点D，与y轴交于点E，与AC交于点F，与抛物线在第二象限交于点G．
（1）求抛物线的解析式；
（2）连接BE，求h为何值时，△BDE的面积最大；
（3）已知一定点M（-2，0）．问：是否存在这样的直线y=h，使△OMF是等腰三角形？若存在，请求出h的值和点G的坐标；若不存在，请说明理由．
数学兴趣小组到外旅游拍一张合影，冲一张底片需1.6元，洗一张照片需0.55元。若每人都得到一张照片，那么平均每人分摊的钱不超过0.7元，问这个小组至少有多少人？
“希望工程”将2000元奖金发给育英中学25名三好学生，其中市级三好学生每人得奖金200元，校级三好学生每人得奖金50元，问全校市级三好学生、校级三好学生各有多少人？
已知关于
的方程
和
的解相同，求
的值。
已知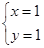
是方程组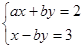
的解，试求
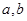的值。
如图所示，△ABC中，∠A=96°。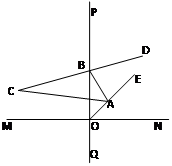
（1）BA1平分∠ABC，CA1平分∠ACD，请你求∠A1的度数；
（2）BA2平分∠A1BC，CA2平分∠A1CD，请你求∠A2的度数；
（3）依次类推，写出∠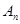
与∠
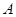的关系式。
（4）小明同学用下面的方法画出了α角：作两条互相垂直的直线MN、PQ，垂足为O，作∠PON的角平分线OE，点A、B分别是OE、PQ上任意一点，再作∠ABP的平分线BD，BD的反向延长线交∠OAB的平分线于点C，那么∠C就是所求的α角，则α的度数为．