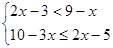己知数轴甲上有A、B、C三点,分别表示-30、-20、0,动点P从点A山发,以每秒1个单位的速度向终点C移动,设点P移动的时间为t秒,点P在数轴甲上表示数P.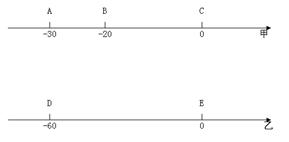
(1)用含t的代数式表示p.
(2)另有一个数轴乙,数轴乙上有D、E两点,分别表示-60、0,点D、E分别在数轴甲上的点A、C的正下方,当点P运动到点B时,数轴乙上的动点Q从点D出发,以点P速度的四倍向点E运动,点Q到达点E后,再立即以同样的速度返回,当点P到达点C时,P、Q两点运动停止,设点Q在数轴乙上表示数q.
①求当点Q从开始运动到运动停止时,p-q的值(用含t的代数式表示);
②求当t为何值时,p=q?
如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF。能否由上面的已知条件证明AB∥ED?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使AB∥ED成立,并给出证明。
供选择的三个条件(请从其中选择一个):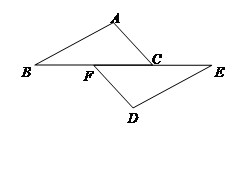
①AB=ED;
②BC=EF;
③∠ACB=∠DFE
如图,在方格纸上建立平面直角坐标系,线段AB的两个端点都在格点上,直线MN经过坐标原点,且点M的坐标是(1,2)。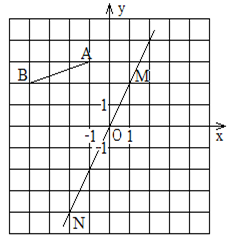
(1)写出点A、B的坐标;
(2)求直线MN所对应的函数关系式;
(3)作出线段AB关于直线MN的对称图形。
如图,已知□ABCD的对角线AC、BD相交于点O,AC =12,BD=18,且△AOB的周长l=23,求AB的长.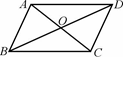
(1)计算: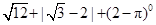
(2)解方程: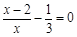 .
.
解方程(不等式组)
(1)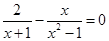
(2)