如图,在方格纸上建立平面直角坐标系,线段AB的两个端点都在格点上,直线MN经过坐标原点,且点M的坐标是(1,2)。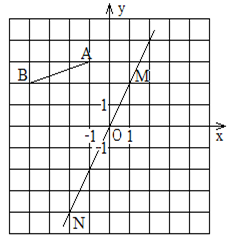
(1)写出点A、B的坐标;
(2)求直线MN所对应的函数关系式;
(3)作出线段AB关于直线MN的对称图形。
如图,小明要测量河内小岛B到河边公路AD的距离,在A点测得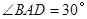 ,在C点测得
,在C点测得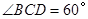 ,又测得
,又测得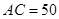 米,求小岛B到公路AD的距离.
米,求小岛B到公路AD的距离.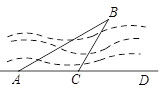
已知:如图,D是AC上一点,DE∥AB,∠B=∠DAE.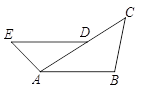
(1)求证:△ABC∽△DAE;
(2)若AB=8,AD=6,AE=4,求BC的长.
已知二次函数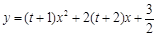 , 在
, 在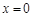 和
和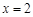 时的函数值相等.
时的函数值相等.
(1)求二次函数的解析式;
(2)若一次函数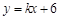 的图象与二次函数的图象都经过点
的图象与二次函数的图象都经过点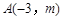 ,求
,求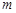 和
和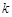 的值;
的值;
(3)设二次函数的图象与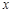 轴交于点
轴交于点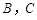 (点
(点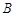 在点
在点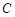 的左侧),将二次函数的图象在点
的左侧),将二次函数的图象在点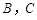 间的部分(含点
间的部分(含点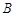 和点
和点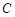 )向左平移
)向左平移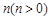 个单位后得到的图象记为
个单位后得到的图象记为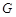 ,同时将(2)中得到的直线
,同时将(2)中得到的直线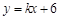 向右平移
向右平移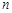 个单位.请结合图象回答:当平移后的直线与图象
个单位.请结合图象回答:当平移后的直线与图象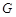 有公共点时,
有公共点时,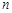 的取值范围.
的取值范围.
已知:⊙O是△ABC的外接圆,点M为⊙O上一点.
(1)如图,若△ABC为等边三角形,BM=1,CM=2,求AM的长;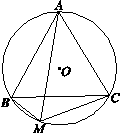
小明在解决这个问题时采用的方法是:延长MC到E,使ME=AM,从而可证△AME为等边三角形,并且△ABM≌△ACE,进而就可求出线段AM的长.
请你借鉴小明的方法写出AM的长,并写出推理过程.
(2)若△ABC为等腰直角三角形,∠BAC=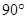 ,
, ,
,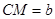 (其中
(其中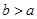 ),直接写出AM的长(用含有a,b的代数式表示).
),直接写出AM的长(用含有a,b的代数式表示).
阅读下面的材料:
小明在学习中遇到这样一个问题:若1≤x≤m,求二次函数 的最大值.他画图研究后发现,
的最大值.他画图研究后发现, 和
和 时的函数值相等,于是他认为需要对
时的函数值相等,于是他认为需要对 进行分类讨论.他的解答过程如下:
进行分类讨论.他的解答过程如下:
∵二次函数 的对称轴为直线
的对称轴为直线 ,
,
∴由对称性可知, 和
和 时的函数值相等.
时的函数值相等.
∴若1≤m<5,则 时,
时, 的最大值为2;
的最大值为2;
若m≥5,则 时,
时, 的最大值为
的最大值为 .
.
请你参考小明的思路,解答下列问题:
(1)当 ≤x≤4时,二次函数
≤x≤4时,二次函数 的最大值为_______;
的最大值为_______;
(2)若p≤x≤2,求二次函数 的最大值;
的最大值;
(3)若t≤x≤t+2时,二次函数 的最大值为31,则
的最大值为31,则 的值为_______.
的值为_______.