沿海开发公司准备投资开发A、B两种新产品,通过市场调研发现:
(1)若单独投资A种产品,则所获利润yA(万元)与投资金额x(万元)之间满足正比例函数关系:yA=kx;
(2)若单独投资B种产品,则所获利润yB(万元)与投资金额x(万元)之间满足二次函数关系:yB=ax2+bx.
(3)根据公司信息部的报告,yA,yB(万元)与投资金额x(万元)的部分对应值如下表所示:
(1)填空:yA= ;yB= ;
(2)若公司准备投资20万元同时开发A、B两种新产品,设公司所获得的总利润为W(万元),试写出W与某种产品的投资金额x(万元)之间的函数关系式;
(3)请你设计一个在(2)中能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少万元?
如图,直线AB:y=﹣x﹣b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.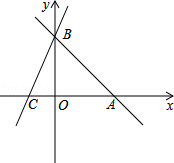
(1)求点B的坐标;
(2)求直线BC的解析式;
(3)直线EF:y=2x﹣k(k≠0)交AB于E,交BC于点F,交x轴于点D,是否存在这样的直线EF,使得S△EBD=S△FBD?若存在,求出k的值;若不存在,请说明理由.
在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E,若AB=5,求线段DE的长.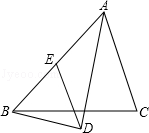
如图,一次函数y=x+1的图象与x轴交于点A,与y轴交于点B,点P位于第一象限且在直线AB上,以PB为一条直角边作一个等腰直角三角形PBC,其中C点位于直线AB的左上方,B点为直角顶点,PC与y轴交于点D.若△PBC与△AOB的面积相等,试求点P的坐标.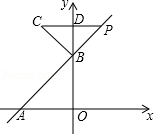
某校八年级两个班的“班级小书库”中各有图书300本.已知2班比1班人均图书多2本,1班的人数比2班的人数多20%.求两个班各有多少人?
已知:图①、图②均为5×6的正方形网格,点A、B、C在格点(小正方形的顶点)上.请你分别在图①、图②中确定格点D,画出一个以A、B、C、D为顶点的四边形,使其为轴对称图形,并画出对称轴.